Апофис: упадет, не упадет?
В статье Википедии «99942 Апофис» говорится: «В 2029 году Апофис должен пройти на минимальном расстоянии около 37500 км от Земли. После проведенных радарных наблюдений возможность столкновения в 2029 году была исключена, однако ввиду неточности начальных данных существует вероятность столкновения данного объекта с нашей планетой в 2036 и последующих годах. Различные исследователи оценивают математическую вероятность столкновения как 2.2×10−5.» Но как же получают эти зловещие оценки?
Орбитальная модель
Оценки вероятности получают на основе математического моделирования орбитального движения. Что такое математическая модель орбиты? На самом деле это просто сводка формул с входящими в них параметрами. В число этих параметров, например, входят время, орбитальные элементы, массы гравитирующих тел и т.д. Формулы дают положение небесного тела на орбите. Таким образом, подставляя соответствующие значения параметров в формулы, получаем положение астероида на любой интересующий момент времени.
Определение параметров модели
Параметры находятся из наблюдений астероида. Как бы тщательно наблюдения не выполнялись, они всегда содержат в себе ошибки (Рис. 1). Поэтому невозможно подобрать такие параметры, которые бы позволяли точно описать наблюдения в рамках выбранной модели. Параметры определяются из принципа наименьших квадратов, т.е., грубо говоря, они подбираются так, чтобы сумма квадратов разностей между наблюдаемыми и моделируемыми величинами на определенные моменты времени была минимальной. Так или иначе, никогда невозможно по наблюдениям получить точные параметры. В итоге можно получить лишь их приближенные оценки. С другой стороны, известно, что в силу случайности ошибок наблюдений при увеличении их количества точность определяемых параметров повышается.

Рис. 1 Из таких наблюдений невозможно получить точные положения астероида
Виртуальные орбиты
Итак, точную орбиту получить невозможно, а только ее приближение. Но тогда встает вопрос: а возможно хотя бы определить, насколько грубой является приближенная орбита и насколько близка реальная орбита астероида к приближенной? Из математической статистики известно, что каким бы не было распределение случайных ошибок наблюдений, оценки определяемых параметров должны быть распределены почти по нормальному многомерному закону. Отнеся этот закон к самим оценкам, мы получаем распределение вероятностной плотности истинных значений параметров относительно их приближенных оценок. На основе этого распределения моделируется множество виртуальных (возможных) орбит (точнее, значений орбитальных параметров): таким образом, плотность распределения полученных значений этих возможных параметров непосредственно соответствует вероятностной плотности их теоретического распределения.
Рис. 2 Виртуальные положения Апофиса (белые точки), полученные на 11-13 апреля 2029 г. по первым наблюдениям
Рис. 3 Виртуальные положения Апофиса (белые точки), полученные на 13 апреля 2029 г. после добавления наблюдений до открытия. Линия голубого цвета - приближенная (номинальная) орбита Апофиса
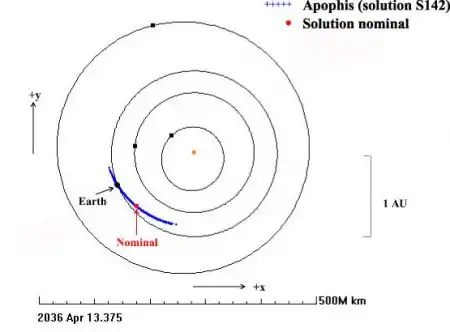
Рис. 4 Виртуальные положения Апофиса (синии точки) на 13 апреля 2036 г.
Оценивание вероятности столкновения астероида с Землей
Наконец, используя орбитальную модель, отображают множество виртуальных орбит на момент сближения астероида и получают распределение возможных положений астероида около планеты. Затем посчитывают число виртуальных астероидов, попавших в тело Земли: шар радиуса приближенно 6400 км. Отношение этого числа к общему числу астероидов дает оценку вероятности столкновения. Очевидно, чем больше рассматриваемых орбит, тем точнее оценка.
Замечания
1. Формально в 2029 г. вероятность столкновения астероида Апофис все же имеется (распределение виртуальных положений астероида определено во всем физическом пространстве), но она ничтожно мала и интерпретируется в прессе как нулевая.
2. Орбита Апофиса еще определена недостаточно точно, чтобы прогнозировать его сближение с Землей в 2036 г., и для этого необходимы дополнительные наблюдения, что позволит уменьшить разброс виртуальных орбит. Однако это совершенно не гарантирует, что после оценка вероятности столкновения уменьшится.
3. Орбиты многих недавно открытых небесных объектов очень плохо определены для прогноза орбитальных положений в будущем. Например, некоторые спутники Юпитера, открытые в 2003, определены настолько плохо, что, скорее всего, будут потеряны. Более того, среди возможных орбит имеются астероидные, т.е. можно говорит, что с определенной вероятностью объект является астероидом.
Пост выполнен по работам отдела небесной механики и астрометрии НИИ ПММ ТГУ (www.astro.tsu.ru).
Рисунки взяты с сайта NASA: neo.jpl.nasa.gov