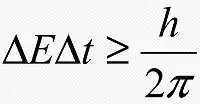Достижения теоретической и экспериментальной физики: квантовая механика - часть первая

Что же послужило предпосылками к пересмотру классических представлений при исследовании микромира? Во-первых, планетарная модель атома, построенная Резерфордом, вроде бы реальная и красивая, противоречила классической электродинамике, согласно которой электрон, движущийся по не важно какой орбите, должен непрерывно излучать световые волны, и, потратив всю свою энергию на это излучение, в конце концов упасть на ядро атома. Но при этом опыты показывали, что непрерывное излучение отсутствует, атомные спектры дискретны, и электрон не падает на ядро, т.е. атом в основном состоянии стабилен. Бор построил квантовую модель атома, которая разрешила противоречия, возникающие в модели Резерфорда, но, тем не менее, наткнулась на определенные сложности в определении спектральных линий уже в самом простом атоме - атоме водорода! Во-вторых, в 19 веке физики с помощью явлений интерференции, дифракции, поляризации света установили, что свет - это волна, но в 20 веке ученые с помощью фотоэффекта и рассеяния света на свободных электронах (комптоновское рассеяние) показали, что свет ведет себя как совокупность частиц с определенной энергией и импульсом. В результате возник знакомый вам корпускулярно-волновой дуализм (КВД), где в одних явлениях свет - это волна, а в других - частица. И только квантовая механика смогла объяснить закономерность КВД. Ну и в-третьих, один ученый еще и усугубил КВД, распространив волновые свойства на частицы, в частности - на электроны. Это был Луи де Бройль. Теперь электрону соответствует определенная волна, характеризуемая частотой колебаний и длиной волны. Волновые свойства электрона были впоследствии подтверждены экспериментами, а позднее были подтверждены волновые свойства и у протонов с нейтронами, и у альфа-частиц! Вот все эти события и подготовили почву для создания квантовой механики.




Что это за название такое - "квантовая"? Это название берет свое начало в самом начале 20 века, когда физик Макс Планк изучал поведение очень горячих тел. Проводя свои эксперименты, он понял, что поведение абсолютно черного тела можно объяснить, если принять, что оно излучает и поглощает свет не непрерывно, а дискретно, порциями. Эти порции Планк и назвал квантами ("quantum" - порция). Правда, Планк не придал своей догадке особого значения и посчитал, что этот эффект обусловлен лишь особенностями внутреннего строения тела, а не природой света. Но Эйнштейн подхватил открытие Планка и пошел дальше, смело заявив, что сам свет распространяется дискретными энергетическими порциями. Эти порции света впоследствии были названы фотонами. Фотон - квант света. Когда фотон взаимодействует с электроном, он может выбить электрон из атома. Это явление называется фотоэлектрическим эффектом, которым Эйнштейн занимался в начале 20 века. Эксперименты показали, что увеличивая интенсивность света, мы увеличиваем лишь количество фотонов, тем самым выбивая большее количество электронов. Но при этом энергия фотонов не меняется. Энергия изменится, если мы изменим частоту излучения, а не его интенсивность. Кстати, официально Эйнштейн получил Нобелевскую премию именно за исследования фотоэффекта, а не за Теорию относительности (хотя и ясно, что значительную часть в этой награде занимает именно последняя, но...как обычно - в дело вмешалась политика). Вот что это за слово такое - квант.

Итак, главными создателями квантовой механики считаются физики Вернер Гейзенберг и Эрвин Шредингер. Их работы в середине 20-х годов 20 века явились ответом практически на все поставленные вопросы. Конечно, принимали непосредственное участие и такие ученые, как Бор, Паули, Дирак, Борн, но они в основном отталкивались от работ Гейзенберга и Шредингера.

Квантовая механика Гейзенберга

Свою основополагающую статью, которая произвела настоящий взрыв в физике, Гейзенберг (кстати, будущий научный руководитель немецкого "Уранового проекта" во время второй мировой) написал на острове в Балтийском море, будучи больным сенной лихорадкой. Он как раз пытался решить проблему определения спектральных линий в атоме водорода. По сути, в своей работе ученый утверждал, что из теории нужно исключить ненаблюдаемые величины и сосредоточиться на установлении соотношений между наблюдаемыми величинами. Что это за величины? Рассматривая свежую, не так давно построенную Бором, квантовую модель атома, к ненаблюдаемым величинам Гейзенберг относил, например, положение электрона в атоме и время его обращения. А наблюдаемыми он считал энергетические уровни в атоме и амплитуды перехода между этими уровнями. Занимаясь построением моделей энергетических уровней и подсчетом вероятностей переходов между ними, Гейзенберг вывел систему уравнений, содержащую как раз амплитуды квантовых переходов, а ненаблюдаемые, по его мнению, величины - в этих уравнениях отсутствовали.




И вот, Гейзенберг посылает работу своему учителю Борну. Борна работа заинтересовала, и через некоторое время появилась уже их совместная работа, где система уравнений Гейзенберга была записана в форме матрицы. Почему в форме матрицы? По мнению ученых, матрица учитывала каждую из наблюдаемых величин, связанных с определенной парой энергетических уровней. Они были правы, потому что из матрицы можно было определить частоту любой спектральной линии в атоме - в зависимости от того, с какого уровня на какой переходит электрон, испуская при этом свет, частота которого и определяется частотой спектральной линии. Например, на рисунке ниже частота спектральной линии v32 определяет частоту света, испускаемого электроном при квантовом скачке с энергетического уровня 3 на энергетический уровень 2. А как интерпретировать частоты, находящиеся в диагонали матрицы (где m=n)? Все просто - эти частоты равны нулю, потому что нет никаких переходов, это один и тот же энергетический уровень. Вот так и удалось решить реальную проблему, стоящую в последнее время перед учеными - вывести спектр энергетических уровней атома водорода - с помощью матричной механики Гейзенберга!




Квантовая механика Шредингера

Хотя матричная механика Гейзенберга и смогла описать стационарные состояния атома и переходы между ними, она не могла решить всех проблем, потому что в этой теории напрочь отсутствовали ненаблюдаемые, по мнению Гейзенберга, величины - траектории частиц. В следующем году Шредингер представил научной общественности свои работы, в которых излагалась новая теория, названная самим автором волновой механикой. Из самого этого названия становится понятно, что ему не нравилась та интерпретация поведения частиц, которая говорила о дискретности, о скачках по уровням - как раз то, на чем была основана матричная механика Гейзенберга. Шредингер, напротив, был сторонником идей де Бройля, который говорил о частице, в частности, электроне, как о волне. Вот на основе этих идей Шредингер и создал свою теорию, которая для физиков оказалась намного проще в использовании, чем матричная механика Гейзенберга. Что это за теория?




Если вы играете (или даже не играете) на гитаре, или на других струнных инструментах, то физический смысл теории Шредингера можно понять, представив колебания натянутой струны. Зажимая струну в двух точках и заставляя ее колебаться, мы получаем звук определенного тона, и далее - обертоны, частота которых - это частота основного тона, умноженная на какое-то целое число. Так вот, Шредингер усматривал здесь аналогию с атомами, полагая, что сами электроны могут рассматриваться как некоторые волновые объекты, подобные колебаниям струны, и свойства этих волновых объектов в каждой точке пространства характеризуются некоторой волновой функцией. И в этой системе спектр частот - это как раз основной тон струны и кратные ему обертоны! В матричной механике этот спектр энергетических уровней имеет структуру посложнее. А что это за волновая функция? Это просто аналог амплитуды колебаний струны. И для своей волновой функции Шредингер написал волновое уравнение, которое вообще, строго говоря, имеет бесчисленное множество решений. Но, раз мы рассматриваем электрон, то волновой процесс должен быть сосредоточен лишь внутри атома, но не вдали от него. Поэтому Шредингер из этого бесчисленного количества решений выбирал лишь те, для которых волновая функция исчезает в точках, бесконечно удаленных от атомного ядра. Это условие и помогло Шредингеру получить искомый результат, и он сразу получил правильное решение для волновой функции в атоме водорода. Кстати, это самое волновое уравнение имеет дифференциальную форму - форму, более привычную для физиков, форму, которой пользовались физики во второй половине 19 века и в начале 20 века. Поэтому неудивительно, что волновая механика оказалась предпочтительней для физиков, чем матричная механика Гейзенберга.

Шредингеру не нравились работы Гейзенберга, и он поражался тому факту, что энергетические уровни, вычисленные двумя способами - его механикой и матричной механикой Гейзенберга - полностью совпадали. И несмотря на то, что ему не нравилась матричная механика, он в конце концов пришел к выводу, что обе эти теории по сути тождественны, отличие состояло лишь в том, что матричная механика исходила из идеи дискретности стационарных состояний, а волновая механика основывалась на волновой непрерывной природе частицы. Этакий пример проявления КВД между разными теориями.

Был еще один человек, который внес свой вклад в развитие обеих теорий. Это уже упомянутый Макс Борн. Про его вклад в матричную механику Гейзенберга мы уже говорили - собственно говоря, именно Борн предложил представить систему алгебраических уравнений Гейзенберга в форме матрицы. Если говорить о волновой механике, то Борну не нравилась чисто волновая интерпретация электрона, он считал, что описание волновых свойств либо неполно, либо неточно. В результате своих размышлений он заявляет, что волновое уравнение Шредингера определяет не материальную волну, а волну вероятности. Т.е. если Шредингер в своей теории полагал, что квадрат волновой функции определяет плотность распределения частицы, размазанной по пространству, то Борн заявлял, что квадрат волновой функции характеризует плотность вероятности для частицы попасть в данную область пространства. Что это означает? А вот здесь в полной мере проявляется различие между классической механикой и квантовой.




Классической механике, как известно, присущ детерминизм - т.е. если известны начальные условия в какой-то момент времени, то вполне можно предсказать, что произойдет в следующий момент времени. В квантовой механике получается совсем другая ситуация. Согласно Борну, даже если мы зададим все начальные условия в какой-то момент времени, решим систему уравнений для волновых функций, мы тем не менее сможем лишь вычислить вероятность тех или иных процессов. В применении к электрону, вероятность обнаружить его в определенном месте может оказаться в несколько раз больше вероятности попадания его в какую-то другую область. Но предсказать его положение со 100%-ной достоверностью уже нельзя. В результате получается, что теперь не приходится говорить об определенной траектории электрона. Теперь электрон оказывается в любом месте внутри атома - как бы размазан по радиусу атома, и корректно говорить о вероятности его нахождения в той или иной области пространства.

Чувствуете разницу между классической и квантовой теориями? Да, в классической физике существует понятие вероятности, но там это понятие возникает, например, по причине большого числа событий. В квантовой механике мы говорим уже о вероятности одиночного события, о поведении одиночного электрона.

Итак, на основе работ Гейзенберга и Шредингера была создана новая теория, объясняющая процессы, происходящие на уровне атома. Каждая из этих теорий была самосогласованна, с той лишь разницей, что волновая механика Шредингера оказалась проще и доступнее для других физиков, нежели теория Гейзенберга. И хотя сам Гейзенберг для своих расчетов зачастую применял именно уравнение Шредингера (ну оно на самом деле проще для физиков!), он тем не менее сильно обижался на своих товарищей, в том числе и на Борна, за то, что они предпочитали использовать для расчетов волновую механику Шредингера. Но, несмотря на такой прорыв в физике, по-прежнему отсутствовало наглядное представление одновременного существования у света и атомных субъектов свойств волны и свойств частицы. Нужно было развивать начатое Гейзенбергом и Шредингером, требовалось разработать новую теорию, наполненную именно объективным физическим смыслом, где все основано на согласии теоретических выкладок, эксперимента, и непротиворечивой логики. И путем пересмотра фундаментальных понятий была разработана такая теория. Она вобрала в себя все основные принципы квантовой механики: принцип неопределенности, принцип соответствия, принцип дополнительности.

Принцип неопределенности

Через 2 года после публикации своих работ по квантовой механике Гейзенберг опубликовал новую статью, содержание которой снова выявило фундаментальное различие между классической и квантовой теориями. Суть статьи заключалась в так называемом принципе неопределенности, согласно которому невозможно измерить одновременно положение и скорость частицы в пространстве. Чем точнее мы пытаемся определить положение частицы, тем больше неточность в определении ее скорости (а значит и импульса). И наоборот. Если (дельта)q - это неточность в определении положения частицы в пространстве, а (дельта)p - неточность в определении ее импульса, то произведение этих величин всегда должно быть больше постоянной планка, деленной на 2(пи). Это и есть знаменитое соотношение неопределенности. Строго говоря, поскольку пространство у нас трехмерное и частица может двигаться в трех осях, то это соотношение должно записываться для всех трех осей - x, y и z (приведено на картинке ниже). Из этого соотношения ясно видно, что чем меньше неточность в определении какого-то из двух параметров, тем больше ошибка в определении второго параметра. Кроме того, Гейзенберг получил, что такое же соотношение связывает и еще две величины - энергию системы и время, потраченное на соответствующее измерение: (дельта)Е х (дельта)t больше h/2(пи). Так каков же физический смысл этих соотношений?





Все мысленные эксперименты Гейзенберга показывали, что принцип неопределенности - это фундаментальный закон Природы. В любых экспериментах существует граница исследований, установленная принципом неопределенности. Почему мы не можем применить законы классической физики к объектам микромира? Это не дает сделать именно соотношение неопределенности. Согласно ему, положение и скорость не могут быть определены одновременно, поэтому произвести расчеты исходя из классической механики невозможно, и понятие траектории частицы теряет смысл. Здесь мы можем говорить лишь о вероятности нахождения частицы в какой-то области пространства. Допустим, мы захотели увидеть электрон, определить его положение. Но чтобы его увидеть, нам нужно направить на него свет. Мы направляем на него свет определенной частоты, но при этом фотон ударяет по электрону, провоцируя его возмущение, непредсказуемое изменение его импульса. Какой бы совершенной ни была аппаратура, с помощью которой мы проводим исследования, границу, установленную принципом неопределенности, обойти невозможно.

А почему мы, например, не чувствуем этой границы в нашем обычном макромире? Почему, когда мы сидим в машине, мы точно знаем ее положение, например, когда стоим на светофоре, но при этом у нас не расплывается стрелка спидометра? Или наоборот - когда мы смотрим на спидометр и точно определяем скорость, мы не расплываемся в пространстве, теряя свое четкое положение? Ответ следует из соотношения неопределенности: потому что постоянная Планка невообразимо мала, она равна 1,05 х 10^-27 эрг*с. Эрг*с - это размерность действия. В макромире, где величина действия во много раз больше постоянной Планка, этой величиной можно пренебречь. В результате наша точность в определении нашего положения или нашей скорости совершенно не влияет на точность в определении второго параметра. Эти точности несравненно грубее величин, характерных для микромира. Здесь, кстати, просматривается принцип соответствия квантовой механики (его ввел Бор): законы квантовой механики стремятся к законам классической механики, когда величина действия становится много большей по сравнению с постоянной Планка.

Для полноты понимания поговорим теперь кратко о мысленных экспериментах, о которых я упоминал выше. Вернемся к определению положения электрона. Для того, чтобы нам его увидеть, мы должны посмотреть на него в микроскоп, пусть это будет самый совершенный микроскоп (мысленные эксперименты ведь не запрещают этого). Чтобы посмотреть на электрон, мы должны направить на него световой луч и поймать отраженный сигнал. Это логично и всем понятно. Кроме того, чтобы нам получить четкое изображение электрона, мы должны направить на него луч довольно большой энергии, т.е. большой частоты и соответственно коротковолновый. Поэтому здесь видимый свет не очень-то и подходит, больше подходит рентгеновский, или даже гамма-луч. При видимом свете мы не увидим электрон, мы получим лишь дифракцию. Итак, наш фотон большой энергии сталкивается с электроном и передает ему часть своего импульса. Т.е. чем точнее мы определяем положение электрона, тем больший импульс мы ему сообщаем. При этом увеличивается не только величина импульса, но и ее неопределенность, причем если мы имеем бесконечно большую энергию луча (бесконечно малую длину волны), то электрон может получить какой угодно импульс, который при этом становится полностью неопределенным.



Рассмотрим еще один мысленный эксперимент, в котором мы посылаем электрон через два отверстия. Прохождение электрона регистрирует фотопластинка. Если мы закроем сначала одно отверстие, электрон пройдет через другое, в определенную точку фотопластинки, расположенную напротив открытого отверстия. Закроем второе отверстие - электрон пройдет через первое, оставив напротив него точку. Откроем теперь оба отверстия. Мы вправе ожидать, что электрон пройдет либо через первое, либо через второе отверстие, оставив точку напротив того отверстия, через которое он пройдет. Но на самом деле получается другая картина - интерференция - последовательность темных и светлых полос. Это означает, что электрон как бы почувствовал, что оба отверстия открыты и в некотором смысле может пройти через оба отверстия. Выходит, что в случае открытых отверстий электрон ведет себя как волна (потому что интерференция говорит о волновой природе объекта), и по интерференционной картине можно определить длину этой волны, а соответственно и импульс электрона (определяется как отношение постоянной Планка к длине волны). При этом вторую компоненту - положение - определить мы не можем, потому что не знаем достоверно - через какое отверстие пройдет электрон. В случае поочередно закрываемых отверстий, когда мы пытаемся, наоборот, закрепить положение электрона, проводя его через то или иное отверстие, он ведет себя как частица, оставляя точку напротив открытого отверстия - интерференционная картина исчезает, и поэтому нет возможности измерить импульс.




В результате, мы приходим к тому, что соотношение неопределенности, по сути, представляет собой математическое выражение КВД, и явление КВД может объясняться только экспериментом! Та проблема, которая оставалась нерешенной даже после первых работ Гейзенберга и Шредингера, постепенно начала разрешаться под натиском самой Природы.

Принцип дополнительности

Принцип дополнительности, так же как и принцип неопределенности, являл собой концепцию объяснения смысла закономерностей квантовой механики. Отличались лишь некоторые аспекты, с позиции которых разрабатывались эти теории.

В упрощенном виде принцип дополнительности заключается в следующих утверждениях: 1. Всю информацию о микромире мы можем получить только с помощью приборов, подчиняющихся законам классической физики. Не существует объективно реального микромира, пока мы не произведем акт наблюдения за ним с помощью наших приборов. Любые процессы, происходящие в микромире, включают в себя взаимодействие с макроскопическим прибором. 2. Характер этого взаимодействия таков, что с помощью каждого конкретного прибора мы можем изучать лишь один конкретный процесс, происходящий в микромире - например, мы можем измерять либо положение частицы, либо ее импульс - но не обе величины одновременно. При этом положение и импульс (ну или энергия и время) - это как бы две половинки одной сущности, которые не конфликтуют друг с другом, а лишь взаимно дополняют друг друга. И здесь принцип дополнительности то же самое утверждает и о КВД: не существует никакого противоречия, все зависит от того, какие эксперименты мы проводим и что при этом наблюдаем. Если мы используем приборы для наблюдения явлений интерференции, дифракции, то здесь частицы проявляют свои волновые свойства. Если мы берем приборы для наблюдения фотоэффекта, мы наблюдаем корпускулярные свойства частиц. Эти два свойства дополняют друг друга, и не существует такого процесса, в котором будут присутствовать сразу оба этих свойства, поскольку в противном случае возникало бы внутреннее противоречие теории.

Если в рамках принципа дополнительности вернуться к мысленному опыту с двумя отверстиями, то можно сказать, что оба этих отверстия являются взаимно дополняющими. Если мы закрываем одно отверстие, мы локализуем частицу (т.е. определяем ее положение - через открытое отверстие), если мы открываем оба отверстия, то наблюдаем интерференцию и определяем импульс частицы, исходя из длины ее волны. Однако одновременно положение и импульс мы не сможем определить с помощью одного этого прибора.

Вот примерно такова суть работ и открытий, которые вместе создали новую область физики - квантовую механику, которая смогла объяснить процессы, происходящие на атомном уровне. Надеюсь, вы поняли суть этих работ. Но это еще не все. Были люди, которые отвергали некоторые принципы квантовой механики, не хотели их принимать и всячески пытались их опровергнуть. "Квантовикам" пришлось отчаянно сражаться и доказывать состоятельность своей теории на протяжении нескольких лет, и, я считаю, эта борьба, как это ни странно, явилась своего рода продолжением развития квантовой механики. Но, чтобы не перегружать голову, об этом поговорим во второй части, в следующем посте. Продолжение следует...