Закон Бенфорда: как выявить обман и мошенничество с помощью математики

Алогичность истории часто заключается в том, что имена первооткрывателей часто забывают. Америго Веспуччи не открывал новых земель, а только доказал, что земли открытые Колумбом являются новым материком, но он как раз получил имя Веспуччи. А о том, что на самом деле Америку открыл викинг Лейф Эрикссон даже среди американцев знают немногие. Так произошло и с закономерностью открытой Ньюкомбом - она получила название "Закон Бенфорда".

История открытия

Астроном, математик и экономист из США Саймон Ньюкомб в 1881 году по долгу службы листал справочник по логарифмам. В наше время логарифм можно взять на любом инженерном микрокалькуляторе, но в 19 веке таблицы логарифмов были для ученых занятых точными науками жизненно необходимыми.




Нькомб обладал проницательным умом (чему свидетельство примерно 400 научных работ) и обратил внимание на странный факт - страницы, где находились логарифмы чисел были изрядно истрепаны, а те страницы где логарифмы начинаются с 9 выглядят почти как новые. Получалось так, что людей, ранее пользовавшихся книгой интересовали числа начинающиеся на 1, и практически не интересовали числа начинающиеся на 9. Объяснить этот феномен Ньюкомб не смог, ведь согласно теории вероятности частота открытия любых страниц должна совпадать. Вскоре о странном открытии забыли.

Повторно обратил внимание на указанный феномен Фрэнк Бенфорд. Он анализировал табличные данные касающиеся абсолютно несвязанных между собой понятий. В число анализа попали бассейны 335 крупнейших рек планеты, удельная теплоемкость различных веществ, уличные номера домов и многое другое. После обработки массива информации стало ясно, что в качестве первой значащей цифры числа 1 появляется с вероятностью 30%. Для числа 2 эта вероятность уменьшается до 18%, а для 9 составляет всего 4,6%.




Поначалу ученые скептически отнеслись к открытию Нькомба-Бенфорда. Анализ различных статистических данных показал, что для привычного всем нормального распределения, такого как распределение IQ людей, закон Бенфорда не работает, он не работает с распределениями с заданными минимальными или максимальными значениями. а также не подходит для распределений, охватывающих только один или два порядка величин. Массив данных должен быть достаточен для применения статистических методов.

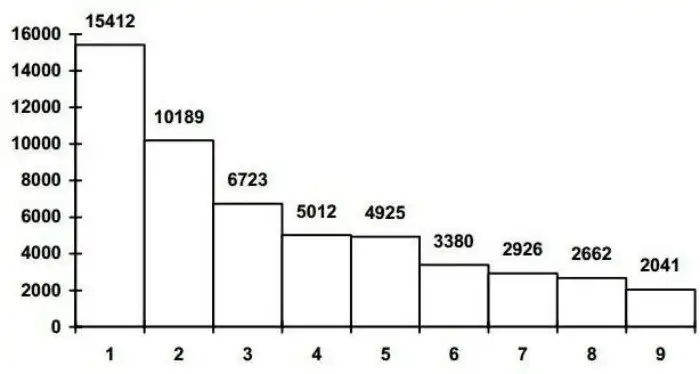
В одной из школ был проведен интересный эксперимент: 40 школьников выписали из статей в различных энциклопедиях 53270 чисел, а затем посчитали частотность появления цифр на первом месте в записи этих чисел, и вот какой результат они получили:




Попытки объяснения закона Бенфорда

Одним из способов объяснить найденную закономерность было следующее вычисление. Путь от 1 к 2 очень большой - он требует увеличения начального числа в 2 раза. Путь от 2 до 3 требует увеличения только на 50% от начального значения величины. А путь от 8 до 9 занимает весьма краткие 12,5% увеличения. Вот и получается, что 1 будет встречаться как первая значимая цифра гораздо чаще.




В 1985 году ученый-физик Дон Лемонс обратил внимание на факт интуитивно известный каждому человеку - луж оказывается гораздо больше чем прудов. Количество прудов тоже значительно больше чем озер, зато число озер превышает количество морей, которых в свою очередь также значительно больше, чем океанов. Так же вполне логично, что озер с площадью зеркала от 1 до 2 километров квадратных значительно больше, чем тех чья площадь зеркала находится в рамках от 8 до 9 квадратных километров. И уж совсем очевидно, что мелкой гальки гораздо больше. чем крупных валунов. Так что по мнению части специалистов закон Бенфорда эмпирически доказала сама природа.

Что интересно, так это то, что закону Бенфорда подчиняются некоторые математические объекты, такие как факториалы, числа Фибоначчи или последовательность степеней двойки.




Впрочем, часть ученых полагает, что никакого закона Бенфорда нет в принципе.

Практическое применение закона

До 1995 года многим казалось, что даже если закон Бенфорда и справедлив, то никакого применения и пользы на практике от него не получишь. Математик из США Марк Нигрини, видимо, был честным налогоплательщиком. Во всяком случае именно в его голову пришла мысль, что данные налоговых деклараций тоже должны подходить под распределение описываемое законом Бенфорда.




Работники налоговой полиции Нью-Йорка заинтересовались идеей Нигрини и проверили часть крупных налогоплательщиков. Внутри имевшегося массива данных было обнаружено несовпадение с распределением по закону Бенфорда, что дало возможность судить о махинациях некоторых контролируемых лиц. дальнейшие действия налоговиков позволили обнаружить в выборке 7 человек скрывающих данные о своих доходах. Проверка налоговых деклараций семейства Клинтонов, сделанная Нигрини ради забавы, подтасовок не обнаружила.

Еще одной сферой применения закона Бенфорда на практике является анализ нарушений при проведении выборов, поскольку данные о них тоже определяются большим массивом голосов.

В целом закон первых чисел можно использовать анализа совершенно разных показателей. Ими могут быть численность населения, длины рек, котировки акций на бирже,

А еще можно устанавливать ведутся ли приписки по сдаче государству, молока, мяса и зерна.