Когда пересекаются параллельные прямые
Из школьного курса геометрии каждому человеку известно, что параллельными именуются прямые, которые не имеют общей точки. Однако это простое утверждение почему-то изредка опровергается различными знакомыми, которые доказывают, что коллинеарные линии могут пересекаться. В реальности, геометрия Евклида, которую преподают в школе не единственный вариант этой науки. При более конкретном исследовании выясняется, что пересечение параллельных прямых зависит от формы поверхности, на которой они проведены. Рассмотрим несколько различных вариантов геометрий, принципиально отличающихся друг от друга.
Геометрия Евклида
Евклид. Источник изображения: istock.com
Это привычная всем геометрия, имеющая историю в не одну тысячу лет. Ее начала были известны еще в Древнем Египте, а аксиомы (постулаты, утверждения) были сформулированы в Древней Греции выдающимся математиком древности Евклидом. Все его утверждения не вызывали сомнений, кроме пятого. Это утверждение показывало, что через точку, лежащую вне прямой, есть возможность провести единственную прямую коллинеарную заданной. Коллинеарные прямые в этом случае не пересекаются. Сумма внутренних углов треугольника равна двум прямым углам. Однако попытки математически доказать 5 постулат Евклида упирались в порочный круг.
Однако житейский опыт дает возможность не совсем верить в справедливость утверждения, что параллельные прямые не пересекаются - если смотреть на ровное железнодорожное полотно, то будет впечатление, что где-то вдалеке параллельные рельсы сойдутся в одну точку. То же самое касается и лучей идущих от точечного источника - тени от разных предметов параллельны, но оставившие их лучи вышли из одной точки.
Приведенные выше рассуждения дали возможность создать проективную геометрию, которая дополняет привычную Евклидову прямую бесконечно удаленной точкой, а на плоскости появляется прямая бесконечно удаленных точек. Вот на этой прямой и пересекаются все коллинеарные прямые.
Геометрия Лобачевского
Николай Иванович Лобачевский. Источник изображения: wikipedia.org
В 19 веке Николай Иванович Лобачевский, а также немец Гаусс и венгр Больяи, предложили геометрию, в которой имеются минимум 2 прямые коллинеарные заданной. Эти прямые пересекаются между собой и приближаются к заданной прямой с двух различных направлений. Место их пересечения с заданной прямой находится в бесконечно удаленной точке. Прямые, которые пересекаются с заданной прямой еще дальше, называются сверхпараллельными.
Наглядно это можно представить, если изобразить плоскость, как овал, и провести внутри него прямую. Линия границы овала будет представлять в таком варианте прямую бесконечно удаленных точек. Затем вне данной прямой зафиксируем точку и проведем через нее 2 прямые, пересекающие заданную на границе овала (то есть на прямой бесконечно удаленных точек). Эти 2 прямые и будут называться параллельными. Те же прямые, которые пересекаются с данной прямой за пределами овала окажутся сверхпараллельными.
Согласно последним научным данным, геометрия Лобачевского имеет место в реальной природе вблизи крупных тяготеющих масс, где само пространство перестает быть плоским и получает кривизну. Сумма углов треугольника в этом варианте не достигает 180 градусов.
Сферическая геометрия и геометрия Римана
Гео́рг Фри́дрих Бе́рнхард Ри́ман — немецкий математик, механик и физик. Источник изображения: wikipedia.org
Тоже в 19 веке немец Риман по-своему проанализировал 5 утверждение Евклида и предположил, что коллинеарных прямых нет в принципе. На основании своего предположения Риман создал геометрию, в которой у всех прямых имеется общая точка, а сумма углов треугольника превышает 180 градусов. Нет в геометрии Римана и понятия, что точка лежит между двумя другими точками. Но это вполне реальная с математической точки зрения геометрия.
Объяснить римановскую геометрию на доступном примере сложно, поэтому имеет смысл обратиться к близкой к ней по множеству характеристик сферической геометрии (правда, здесь параллельные прямые пересекаются сразу в 2 точках).
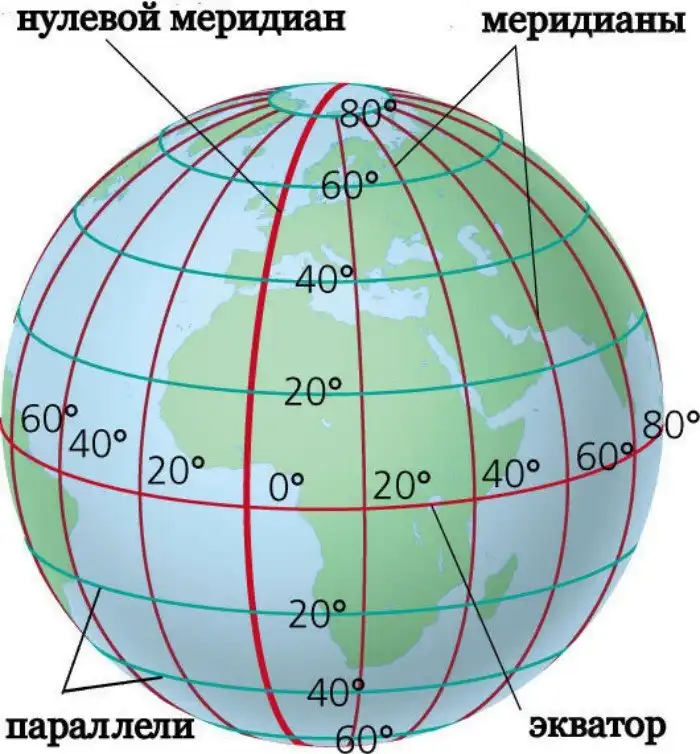
параллели и меридианы. Источник изображения: m-globe.ru
Рассмотрим в качестве сферы нашу планету Земля. Как одну из прямых возьмем экватор, а в качестве коллинеарных между собой прямых будем считать меридианы. Они коллинеарны друг относительно друга, поскольку пересекают экватор под прямым углом (углом между пересекающимися линиями в математике является угол между их касательными, проведенными в точке пересечения данных линий). Однако известно, что меридианы пересекаются на полюсах.
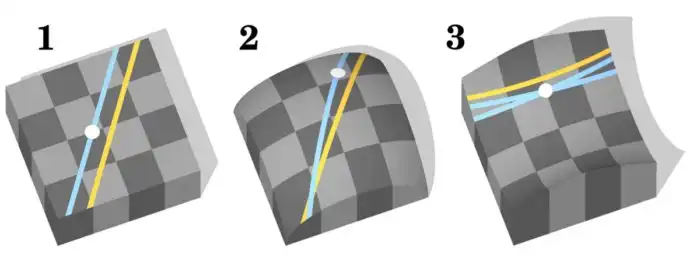
(1) евклидова геометрия; (2) геометрия Римана; (3) геометрия Лобачевского. Источник изображения: wikipedia.org
Общим выводом, ради которого была написана статья, является утверждение, что нельзя достоверно сказать, пересекаются параллельные прямые или нет, если дополнительно не указывать, какой из видов геометрии имеется в виду.