Невообразимое «число Шеннона»
Даже Остап Бендер минимум два раза в своей жизни играл в шахматы. Обычный человек в своей жизни делает это гораздо чаще, ведь древняя игра до сих пор остается одной из самых популярных в мире. Мастера спорта по шахматам, а тем более гроссмейстеры, хорошо знают шахматную теорию и представляют развитие партии на 5-7, а бывает и больше, начальных ходов. Но даже и эти знатоки игры иногда в первых ходах партии сталкиваются с неожиданностями преподнесенными партнерами по матчу.
Источник изображения: depositphotos.com
Неожиданности в самом начале партии являются закономерным явлением, ведь теоретически на доске существует свыше 9 миллионов различных позиций только после 3 полных ходов белых и черных. А дальше их количество лавинообразно продолжает нарастать.
Американский математик Клод Шеннон заинтересовался, сколько различных неповторяющихся шахматных партий можно сыграть.
Клод Элвуд Шеннон. Источник изображения: Wikimedia.org
В 1950 году он опубликовал результат своих вычислений, у него получилось число примерно 10^ 120!
Нематематикам даже прочитать это сложно. Читается это как «десять в сто двадцатой степени», а пишется без показателя степени как 1, а за ней 120 цифр 0. Правда даже математикам практически невозможно осознать величину этого числа (автор статьи знает это по себе). Написать на бумаге 10^120 можно, но прочувствовать его величину невозможно.
Насколько велико число Шеннона и как он его рассчитал?
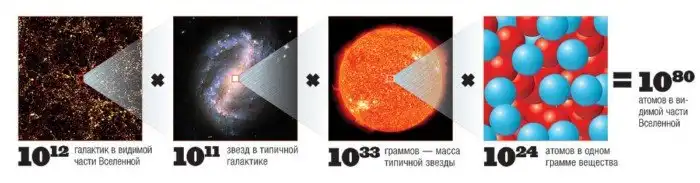
Поскольку Клод Шеннон первым вычислил количество неповторяющихся партий, то и определенное им значение получило название «число Шеннона». Чтобы осознать величину этого числа можно вспомнить, что количество атомов в наблюдаемой Вселенной колеблется в пределах от до 10^80 единиц. То есть, число Шеннона примерно в 10^40 больше общего количества атомов.
Количество атомов в видимой части Вселенной. Источник изображения: liveinternet.ru
В своих расчетах Шеннон исходил из того, что средняя партия длится 40 ходов. В каждый из моментов игрок выбирает примерно из 30 различных возможностей. Условность вычислений сразу становится понятной, если учесть, что самая длинная официальная партия между Иваном Николичем и Гораном Арсовичем затянулась на целых 269 ходов. Было это в Белграде в 1989 году, а непосредственно за шахматным столом игроки провели 20 ч 15 мин, да еще и сыграли вничью. А ведь позиции, в которых у игрока имеется в запасе значительно больше 30 различных ходов далеко не редкость.
Источник изображения: sociviews.com
Итак, количество неповторяющихся шахматных партий вычислено. Хотя точность подсчетов и невелика, но все же число определено, дело сделано. Клод Шеннон решил пойти дальше и определить количество возможных позиций на доске, которые могут встретиться в реальной партии. Задача еще сложнее, чем кажется на первый взгляд. На шахматной доске имеется много различных позиций, которые можно поставить, поскольку они не противоречат правилам игры, но встретиться в реальной партии между двумя игроками они не могут ни при каких условиях. Даже весьма посредственный шахматист может поставить двух коней и короля так, что они поставят мат одинокому монарху. Но в реальности эта позиция недостижима, хотя иногда и используется в шахматной композиции.
Источник изображения: hal.sistema-decimal.info
Требовалось создать дерево возможной игры по правилам шахмат, так чтобы отсечь невозможные позиции. Эта была гигантская по сложности задача, но Шеннон очень любил красоту шахмат. Математику удалось учесть большое количество факторов. После приблизительных вычислений он получил, что количество неповторяющихся шахматных позиций в реальной игре примерно равняется 10^43 единиц.
Однако все ситуации, запрещенные согласно современных правил игры, исключить не удалось. Поэтому в последние 3 десятилетия появились работы уточняющие количество теоретически возможных позиций. А некоторые работы и вовсе опровергают число в 10^43.
А вот число Шеннона под сомнение пока не ставят и оно по-прежнему 10^120.