Геометрическая задача: какого цвета был медведь?
Начнём с обычно вызывающей хохот в классе математической задачки: «Охотник проснулся, вышел из палатки, прошёл по прямой 5 километров на юг, потом по прямой 5 километров на восток, застрелил медведя, прошёл по прямой ещё 5 километров на север и вернулся в свою палатку. Какого цвета был медведь?» .
Если вы против жестокого обращения с животными, можно считать, что охотник, встретив медведя, перепугался, потерял ружьё и убежал – сути задачи это не меняет.
С первого взгляда эта задачка кажется бредом. Типа «Плывут по Нилу два крокодила, один зелёный, другой на север». Но на самом деле задачка про медведя вполне себе серьёзная и решается!
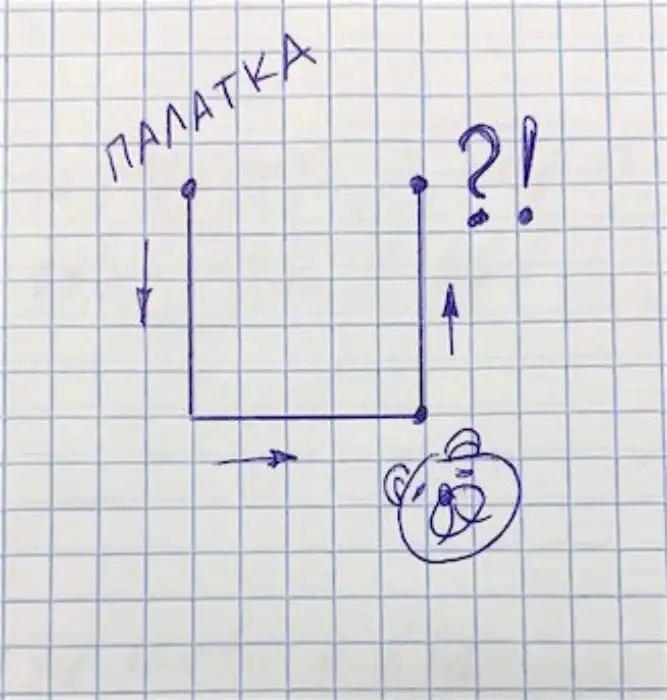
Вспоминаем, что направления «север-юг» и «запад-восток» перпендикулярны друг другу, то есть угол между ними составляет 90 градусов. Возьмём лист бумаги в клетку и карандаш и попробуем нарисовать маршрут охотника. Сперва «вниз», то есть на юг, 5 километров – то есть 5 клеточек. Потом «вправо», то есть на восток, 5 клеточек. Потом «вверх», на север – ещё 5 клеточек. Внимательно смотрим на наш незатейливый чертёжик и думаем.
На листе бумаги у нас получается разомкнутая линия! А по условию задачи охотник вернулся «в свою палатку», то есть в ту же точку, из которой вышел. Линия, получается, должна быть замкнутой ... Может ли такое быть вообще? А?
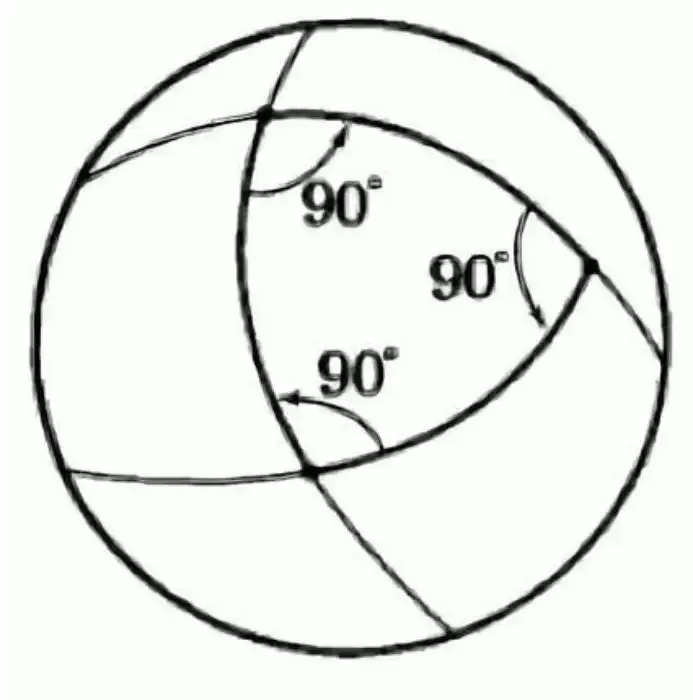
«Не может!» – скажут те, кто на уроках геометрии хотя бы иногда слушал учительницу. «Если охотник вернулся туда, откуда вышел, тогда его путь представляет собой треугольник, три соединённых собой отрезка прямых. Но все повороты охотника – по 90 градусов, и тогда у нас получается, что сумма углов треугольника должна быть 3 х 90 = 270 градусов. А сумма углов треугольника всегда составляет 180 градусов!».
Прекрасный ответ, пятёрка! И вот как раз здесь возникает сумасшедший (на первый взгляд) вопрос: а может ли быть такое, что сумма углов треугольника может составлять 270 градусов, и это не противоречит законам геометрии?
Может! Такая геометрия существует , причём это не какая-то там «геометрия Лобачевского», придуманная относительно недавно и плохо понятная простым людям. Эта геометрия известна больше 2500 лет, ею успешно занимались ещё древние греки. Называется она «сферическая геометрия» , или «сферика». Чем-то эта геометрия похожа на школьную – в ней есть точки, отрезки, линии, углы, треугольники, периметры, площади... Однако есть и разница, да какая!
Например, в школьной геометрии мы учим: «Через точку, не лежащую на прямой, можно провести одну и только одну прямую, параллельную данной» . А сферическая геометрия говорит совершенно другое: «Через точку, не лежащую на прямой, нельзя провести ни одной прямой, параллельной данной. Любые две несовпадающие прямые пересекаются в двух точках» .
То есть: параллельных прямых там не существует вообще! А для двух прямых существуют две разные точки пересечения!
А вот ещё пример. Школьная геометрия: «Сумма углов треугольника всегда равна 180 градусам» . А вот сферическая геометрия: «Сумма углов треугольника всегда больше 180 градусов и меньше 540 градусов» .
А ещё в сферической геометрии есть вот какая теорема: «Сумма сторон треугольника всегда меньше 360 градусов». И не спешите возражать, что стороны треугольника и вообще отрезки в градусах не измеряют – ещё как измеряют...
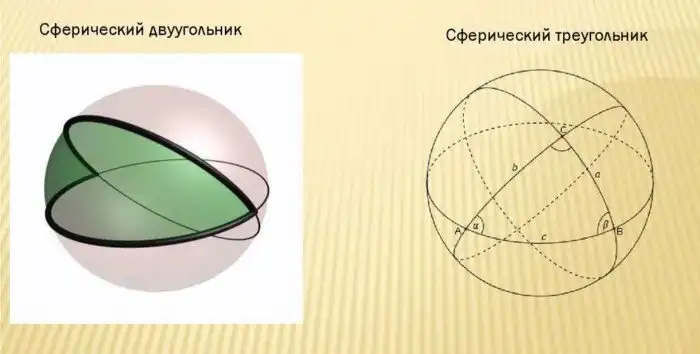
А ещё в сферической геометрии существует геометрическая фигура «двухугольник» . Это замкнутая фигура, которая образована двумя пересекающимися отрезками прямых и двумя углами между этими прямыми.
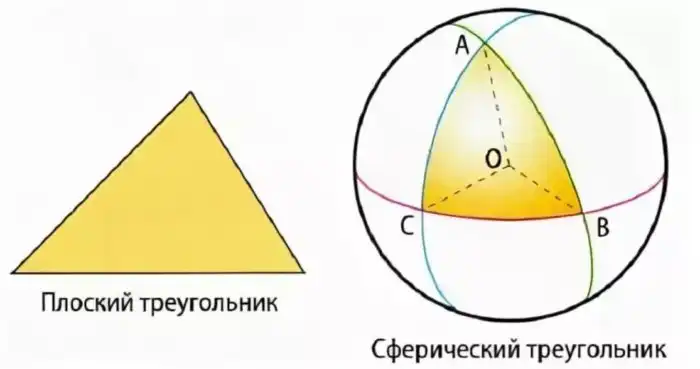
Ключ к загадке – «сфера». Школьная геометрия называется «планиметрия», то есть это геометрия на плоской поверхности. А если мы возьмём мяч или глобус и начнём на нем проводить линии и строить фигуры, то быстро убедимся, что все «сумасшедшие» законы и теоремы, приведённые выше, прекрасно выполняются!
Как же решается задача о медведе? Путь охотника представляет собой треугольник с суммой углов 270 градусов – то есть сферический треугольник. Значит, действие задачи происходит на поверхности сферы, «на глобусе». А где у нас на глобусе заданные в условии направления на север и юг (то есть меридианы) могут пересекаться между собой под углом 90 градусов (и вообще пересекаться под углом)? Таких точек только две – это северный и южный полюса! Так что палатка охотника находилась на северном полюсе, и медведь был полярный, то есть белый!
Для проверки возьмите глобус и карандашом проведите путь охотника – от северного полюса вдоль меридиана на юг, затем вдоль параллели такое же расстояние на восток, затем вдоль меридиана обратно на север – и вернётесь в ту же самую точку!
Почему сферическую геометрию не учат в школе? Почему её начинают преподавать только в высших учебных заведениях (или в морских училищах)? Во-первых, сложновата. А во-вторых, школьникам и одной планиметрии хватает, чтобы ломать голову над задачками и получать двойки, не правда ли? Вот заботливые взрослые и убрали сферику из школьной программы, чтобы «не мучить бедных деток» – хотя этой наукой успешно занимались ещё Эвклид, Архимед, Евдокс, Птолемей и прочие древнегреческие математики. А на практике широко применяется эта наука прежде всего в географии , астрономии и навигации (мореплавании).