«Парадокс береговой линии»: феномен, который уже более 70 лет является неразрешимой проблемой для географов и картографов
Чем протяженнее общая граница между двумя государствами, тем выше вероятность вооруженного столкновения между ними, и это логично, ведь всегда могут найтись какие-то спорные территории, да и попросту больше вероятность случайного приграничного конфликта. Но предположение не есть доказанный факт. Этот вопрос в 1951 году решил изучить Льюис Фрай Ричардсон, а за образец стран он взял Португалию и Испанию.
И тут неожиданно выяснилось, что протяженность общей границы неизвестна. То есть, граница существует и хорошо изучена, но чему равна ее длина неизвестно. Португалия оценивала эту величину в 987 км, а по испанской версии она составляла 1214 км. Это несовпадение дало импульс к изучению проблемы измерения береговой линии, но оказалось, что ее парадоксально просто невозможно измерить.
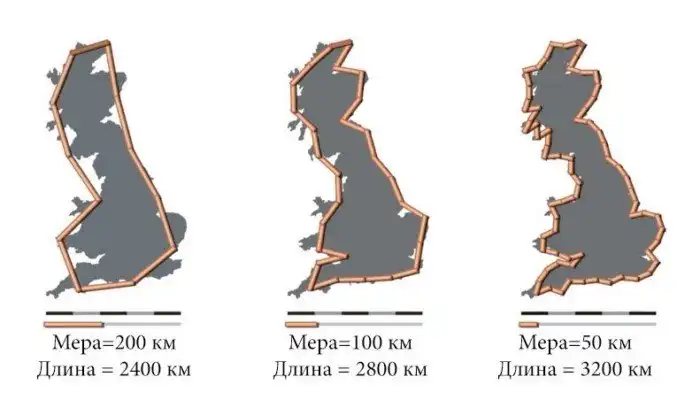
Как привычным способом измеряют береговую линию? Выбирают некий единичный отрезок и накладывают его при посредстве циркуля на географическую карту столько раз, сколько потребуется для создания ломаной линии, закрывающую очертания побережья. Вот тут и проявляется парадокс береговой линии — ее длина зависит от величины выбранного единичного отрезка.
Парадокс береговой линии
Измерение линии побережья Великобритании с шагом в 200 км дает результат 2400 км. Когда за меру измерения взять отрезок в 100 км, то британская береговая линия увеличивается до 2800 км. В случае уменьшения мерного отрезка еще вдвое измеряемая величина становится уже около 3200 км.
Протяженность береговой линии при измерении отрезками разной длины
Из приведенных выше результатов становится очевидно, что уменьшение отрезка измерения обратно пропорционально длине береговой линии. Первоначально Ричардсон ожидал, что несмотря на увеличение размеров береговой линии при уменьшении меры измерения наступит какой-то предел.
Так в математике если взять вписанный в окружность правильный многоугольник и увеличивать число сторон (длина каждой конкретной стороны при этом уменьшается), то при очень большом их количестве многоугольник практически сольется с самой окружностью, а периметр вписанного многоугольника фактически станет равным длине, описанной окружности. А эта длина конечна и элементарно вычисляется по формуле L=2ПR.
Но в случае с береговой линией все оказалось гораздо сложнее. Гладкую кривую, которую можно приближенно представить в виде большого количества отрезков называют в математике спрямляемой, но береговая линия спрямляемой не является.
Ричардсон пришел к выводу, что поскольку береговая линия не является спрямляемой, то при уменьшении единичного отрезка до бесконечно малого (а анализ бесконечно малых величин является важнейшей областью математики), длина береговой линии возрастает до бесконечно большой величины.
Прошло больше десятка лет после работы Ричардсона, и проблемой измерения длины береговой линии занялся Бенуа Мандельброт. Чтобы относительно детальнее разобраться в вопросе, Мандельброт создал новый раздел математики — фрактальную геометрию. Эта наука описывает неспрямляемые линии, существующие в природе. Основным свойством фракталом является их подобие самим себе с уменьшением масштаба. Полное совпадение самоподобия необходимым не является, но близкое подобие - это обязательное условие.
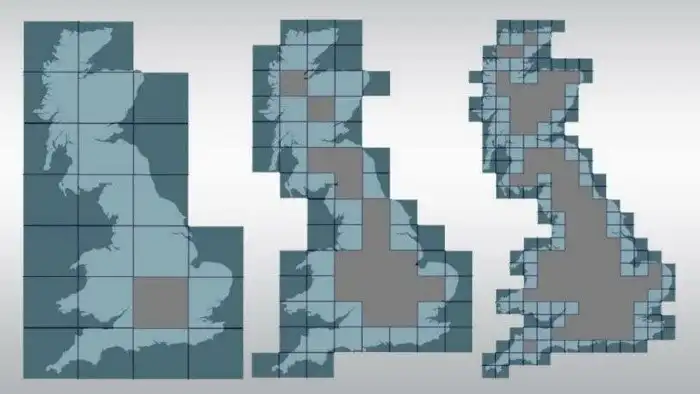
Объяснить это нематематикам сложно, но можно привести пример самоподобия исходя из все той же береговой линии. В выбранном масштабе (пусть 200 км) она состоит из мысов, заливов. Но при уменьшении масштаба до 100 км мы увидим ту же картину мысов и заливов. Но и при дальнейшем уменьшении представиться точно та же картина мысов и заливов. Они, конечно, будут меньше, чем при большом масштабе, но механизм подобия сохранится.
Стоит перейти на масштаб песчинок (а на бытовом уровне подобное не имеет смысла), как там окажется хаотическое расположение своих заливов и мысов, причем береговая линия начнет изменяться мгновенно, превратившись в потенциально бесконечную. Причем расположение мысов и заливов окажется стохастическим.
А теперь коснемся реальных береговых линий отдельных стран. На практике измеряют береговую линию в километрах, а объекты значительно меньшие по своему размеру попросту не учитывают. Правда, с Норвегией и ее фьордами даже условно разобраться сложно.
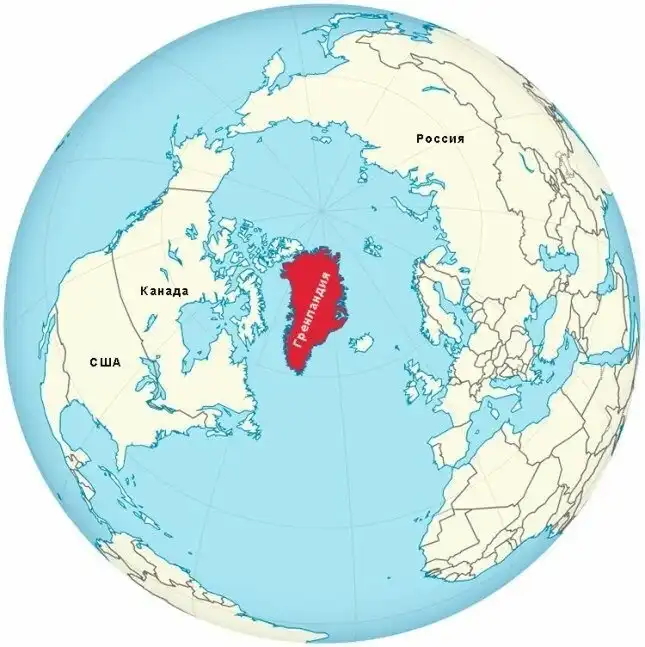
Протяженность береговой линии о. Гренландия больше, чем протяженность береговой линии России
Многие полагают, что раз Российская Федерация имеет наибольшую территорию, то и береговая линия у нее наибольшая. Но это далеко не так. Лидером в столь оригинальной номинации является Канада с береговой линией в 202 080 км, на втором месте устроилась Индонезия 54 716 км, третья Дания в совокупности с Гренландией 7 314 км + 44 087 км и только четвертая Россия 37 653 км.
Ну и в качестве бонуса, немного юмора в тему:
Источник изображения: smbc-comics.com
Источник изображения: smbc-comics.com
Источник изображения: smbc-comics.com
Источник изображения: smbc-comics.com