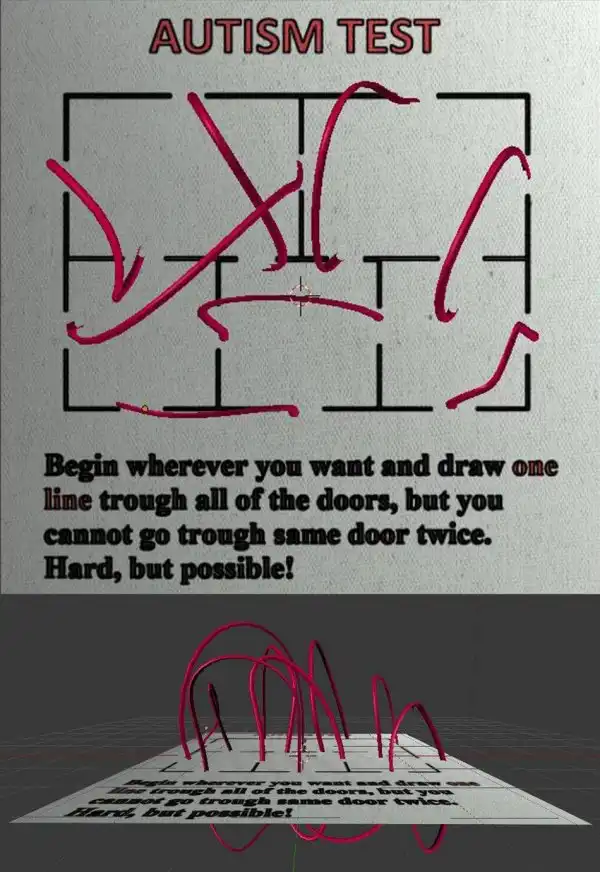
Можно ли пройти этот лабиринт ?

Вы пробовали проходить этот лабиринт ?

Давайте выясним подробнее этот вопрос...

Еще при упоминании этого лабиринта уточняется, что «Аутист способен обрабатывать визуальную и текстовую информацию в несколько раз быстрее, чем человек, не страдающий заболеваниями аутического спектра. Эта их особенность оказалась незаменимой в хайтеке. В датской компании Specialisterne, специализирующейся на технологическом консультировании, 75 процентов работников — аутисты и люди, у которых диагностирован синдром Аспергера, также относящийся к аутическому спектру. От обычных работников они отличаются невероятным вниманием к деталям, сверхчеловеческой сосредоточенностью, способностью быстро обрабатывать огромные массивы информации. Эти умения особенно полезны для тестировщиков программ. Качество работы аутистов, занимающихся этой работой, в несколько раз выше, чем качество работы обычных людей. Аутисты могут проверить техническую документацию на 4000 страниц в 10 раз быстрее обычных людей и не пропустить ни одной ошибки.»



Задача нерешаема! У нас 3 комнаты с нечетным количеством дверей (аналогия с рисунками «не отрывая карандаша»). Что бы задача имела решение необходимо, что бы было не более 2 точек( в нашем случае комнат) с нечетным количеством линий (в нашем случае проходов)

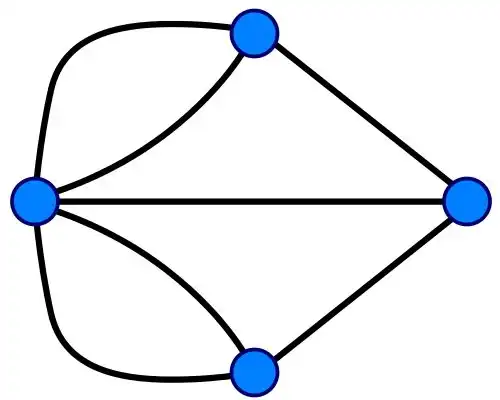
Если построить граф этого лабиринта, то мы увидим, что это Эйлеров путь, так как у него 3 вершины с нечётным числом рёбер (дверей), а для выполнения условий теста их может быть только две.



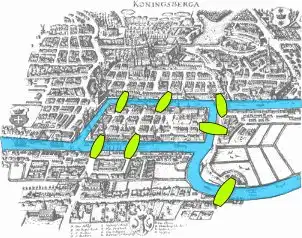
Проблема семи мостов Кёнигсберга или Задача о кёнигсбергских мостах (нем. Königsberger Brückenproblem) — старинная математическая задача, в которой спрашивалось, как можно пройти по всем семи мостам Кёнигсберга, не проходя ни по одному из них дважды. Впервые была решена в 1736 году немецким и русским математиком Леонардом Эйлером.

Издавна среди жителей Кёнигсберга была распространена такая загадка: как пройти по всем мостам (через реку Преголя), не проходя ни по одному из них дважды. Многие кёнигсбержцы пытались решить эту задачу как теоретически, так и практически, во время прогулок. Впрочем, доказать или опровергнуть возможность существования такого маршрута никто не мог.

В 1736 году задача о семи мостах заинтересовала выдающегося математика, члена Петербургской академии наук Леонарда Эйлера, о чём он написал в письме итальянскому математику и инженеру Мариони от 13 марта 1736 года. В этом письме Эйлер пишет о том, что он смог найти правило, пользуясь которым, легко определить, можно ли пройти по всем мостам, не проходя дважды ни по одному из них. Ответ был «нельзя».



На упрощённой схеме части города (графе) мостам соответствуют линии (дуги графа), а частям города — точки соединения линий (вершины графа). В ходе рассуждений Эйлер пришёл к следующим выводам:

• Число нечётных вершин (вершин, к которым ведёт нечётное число рёбер) графа должно быть чётно. Не может существовать граф, который имел бы нечётное число нечётных вершин.
• Если все вершины графа чётные, то можно, не отрывая карандаша от бумаги, начертить граф, при этом можно начинать с любой вершины графа и завершить его в той же вершине.
• Граф с более чем двумя нечётными вершинами невозможно начертить одним росчерком.

Граф кёнигсбергских мостов имел четыре (синим) нечётные вершины (то есть все), следовательно, невозможно пройти по всем мостам, не проходя ни по одному из них дважды.



Созданная Эйлером теория графов нашла очень широкое применение в транспортных и коммуникационных системах (например, для изучения самих систем, составления оптимальных маршрутов доставки грузов или маршрутизации данных вИнтернете).

В 1905 году был построен Императорский мост, который был впоследствии разрушен в ходе бомбардировки во время Второй мировой войны. Существует легенда о том, что этот мост был построен по приказу самого кайзера, который не смог решить задачу мостов Кёнигсберга и стал жертвой шутки, которую сыграли с ним учёные умы, присутствовавшие на светском приёме (если добавить восьмой мост, то задача становится разрешимой). На опорах Императорского моста в 2005 году был построенЮбилейный мост. На данный момент в Калининграде семь мостов, и граф, построенный на основе островов и мостов Калининграда, по-прежнему не имеет эйлерова пути





Посмотрим на картинку 1: окружим квадратами каждую отдельную часть, исключим «лишние» точки, т.е. те точки, использование которых повысило бы возможное количество путей, и исключение которых не повлияет на количество дверей, пройденных линией и замкнутость контура. За начало пути возьмем, к примеру, точку 2.

Посмотрим на картинку 2: на ней я изобразил тот же контур, но так, чтобы были виднее связи начальной точки с последующими. На изображении явно видно, что часть контура, обведенная синим цветом не может быть единожды замкнута, т.е. даже если бы эта часть контура была единственна, то не существовало бы путей, по которым можно было бы построить замкнутую линию.

Итог: задача не имеет решения в двумерной системе координат.