Теория струн для чайников

Но оказалось, что самое удобное количество измерений, необходимое для работы этой теории — целых десять (девять из которых — пространственные, и одно — временное)! Если измерений больше или меньше, математические уравнения дают иррациональные результаты, уходящие в бесконечность — сингулярность.

Следующий этап развития теории суперструн — М-теория — насчитала уже одиннадцать размерностей. А ещё один её вариант — F-теория — все двенадцать. И это вовсе не усложнение. F-теория описывает 12-мерное пространство более простыми уравнениями, чем М-теория — 11-мерное.

Конечно, теоретическая физика не зря называется теоретической. Все её достижения существуют пока что только на бумаге. Так, чтобы объяснить почему же мы можем перемещаться только в трёхмерном пространстве, учёные заговорили о том, как несчастным остальным измерениям пришлось скукожиться в компактные сферы на квантовом уровне. Если быть точными, то не в сферы, а в пространства Калаби-Яу. Это такие трёхмерные фигурки, внутри которых свой собственный мир с собственной размерностью. Двухмерная проекция подобный многообразий выглядит приблизительно так:



Таких фигурок известно более 470 миллионов. Которая из них соответствует нашей действительности, в данный момент вычисляется. Нелегко это — быть теоретическим физиком.

Да, это кажется немного притянутым за уши. Но может, именно этим и объясняется, почему квантовый мир так отличается от воспринимаемого нами.

Давайте немного окунемся в историю

В 1968 г. молодой физик-теоретик Габриэле Венециано корпел над осмыслением многочисленных экспериментально наблюдаемых характеристик сильного ядерного взаимодействия. Венециано, который в то время работал в ЦЕРНе, Европейской ускорительной лаборатории, находящейся в Женеве (Швейцария), трудился над этой проблемой в течение нескольких лет, пока однажды его не осенила блестящая догадка. К большому своему удивлению он понял, что экзотическая математическая формула, придуманная примерно за двести лет до этого знаменитым швейцарским математиком Леонардом Эйлером в чисто математических целях – так называемая бета-функция Эйлера, – похоже, способна описать одним махом все многочисленные свойства частиц, участвующих в сильном ядерном взаимодействии. Подмеченное Венециано свойство давало мощное математическое описание многим особенностям сильного взаимодействия; оно вызвало шквал работ, в которых бета-функция и ее различные обобщения использовались для описания огромных массивов данных, накопленных при изучении столкновений частиц по всему миру. Однако в определенном смысле наблюдение Венециано было неполным. Подобно зазубренной наизусть формуле, используемой студентом, который не понимает ее смысла или значения, бета-функция Эйлера работала, но никто не понимал почему. Это была формула, которая требовала объяснения.

Габриеле Венециано (Gabriele Veneziano)

Положение дел изменилось в 1970 г., когда Йохиро Намбу из Чикагского университета, Хольгер Нильсен из института Нильса Бора и Леонард Сасскинд из Станфордского университета смогли выявить физический смысл, скрывавшийся за формулой Эйлера. Эти физики показали, что при представлении элементарных частиц маленькими колеблющимися одномерными струнами сильное взаимодействие этих частиц в точности описывается с помощью функции Эйлера. Если отрезки струн являются достаточно малыми, рассуждали эти исследователи, они по-прежнему будут выглядеть как точечные частицы, и, следовательно, не будут противоречить результатам экспериментальных наблюдений. Хотя эта теория была простой и интуитивно привлекательной, вскоре было показано, что описание сильного взаимодействия с помощью струн содержит изъяны. В начале 1970-х гг. специалисты по физике высоких энергий смогли глубже заглянуть в субатомный мир и показали, что ряд предсказаний модели, основанной на использовании струн, находится в прямом противоречии с результатами наблюдений. В то же время параллельно шло развитие квантово-полевой теории – квантовой хромодинамики, – в которой использовалась точечная модель частиц. Успехи этой теории в описании сильного взаимодействия привели к отказу от теории струн.
Большинство специалистов по физике элементарных частиц полагали, что теория струн навсегда отправлена в мусорный ящик, однако ряд исследователей сохранили ей верность. Шварц, например, ощущал, что «математическая структура теории струн столь прекрасна и имеет столько поразительных свойств, что, несомненно, должна указывать на что-то более глубокое»2). Одна из проблем, с которыми физики сталкивались в теории струн, состояла в том, что она, как казалось, предоставляла слишком богатый выбор, что сбивало с толку. Некоторые конфигурации колеблющихся струн в этой теории имели свойства, которые напоминали свойства глюонов, что давало основание действительно считать ее теорией сильного взаимодействия. Однако помимо этого в ней содержались дополнительные частицы-переносчики взаимодействия, не имевшие никакого отношения к экспериментальным проявлениям сильного взаимодействия. В 1974 г. Шварц и Джоэль Шерк из французской Высшей технической школы сделали смелое предположение, которое превратило этот кажущийся недостаток в достоинство. Изучив странные моды колебаний струн, напоминающие частицы-переносчики, они поняли, что эти свойства удивительно точно совпадают с предполагаемыми свойствами гипотетической частицы-переносчика гравитационного взаимодействия – гравитона. Хотя эти «мельчайшие частицы» гравитационного взаимодействия до сих пор так и не удалось обнаружить, теоретики могут уверенно предсказать некоторые фундаментальные свойства, которыми должны обладать эти частицы. Шерк и Шварц обнаружили, что эти характеристики в точности реализуются для некоторых мод колебаний. Основываясь на этом, они предположили, что первое пришествие теории струн закончилось неудачей из-за того, что физики чрезмерно сузили область ее применения. Шерк и Шварц объявили, что теория струн – это не просто теория сильного взаимодействия, это квантовая теория, которая, помимо всего прочего, включает гравитацию).



Физическое сообщество отреагировало на это предположение весьма сдержанно. В действительности, по воспоминаниям Шварца, «наша работа была проигнорирована всеми». Пути прогресса уже были основательно захламлены многочисленными провалившимися попытками объединить гравитацию и квантовую механику. Теория струн потерпела неудачу в своей первоначальной попытке описать сильное взаимодействие, и многим казалось бессмысленным пытаться использовать ее для достижения еще более великих целей. Последующие, более детальные исследования конца 1970-х и начала 1980-х гг. показали, что между теорией струн и квантовой механикой возникают свои, хотя и меньшие по масштабам, противоречия. Создавалось впечатление, что гравитационная сила вновь смогла устоять перед попыткой встроить ее в описание мироздания на микроскопическом уровне.
Так было до 1984 г. В своей статье, сыгравшей поворотную роль и подытожившей более чем десятилетние интенсивные исследования, которые по большей части были проигнорированы или отвергнуты большинством физиков, Грин и Шварц установили, что незначительное противоречие с квантовой теорией, которым страдала теория струн, может быть разрешено. Более того, они показали, что полученная в результате теория обладает достаточной широтой, чтобы охватить все четыре вида взаимодействий и все виды материи. Весть об этом результате распространилась по всему физическому сообществу: сотни специалистов по физике элементарных частиц прекращали работу над своими проектами, чтобы принять участие в штурме, который казался последней теоретической битвой в многовековом наступлении на глубочайшие основы мироздания.
Я начал работу в аспирантуре Оксфордского университета в октябре 1984 г. Хотя я был восхищен раскрывавшимися передо мной достижениями квантовой теории поля, калибровочной теории и общей теории относительности, среди моих старших коллег-аспирантов было распространено скептическое убеждение, что большая часть открытий физики элементарных частиц уже сделана. Была разработана стандартная модель, и замечательный успех, с которым она предсказывала результаты экспериментов, оставлял мало сомнений в том, что ее полное подтверждение является делом не слишком отдаленного будущего. Выход за ее пределы для включения гравитации и возможного объяснения экспериментальных данных, на которых базируется эта модель (т.е. 19 чисел, характеризующих массы элементарных частиц, их константы взаимодействия и относительную интенсивность взаимодействий, известных из результатов экспериментов, но не объясненных теоретически), казался такой непосильной задачей, что лишь самые бесстрашные исследователи отваживались принять этот вызов. Однако спустя всего шесть месяцев настроения радикально изменились. Весть об успехе Грина и Шварца, в конце концов, дошла даже до аспирантов первого года обучения, и на смену прежнему унынию пришло возбуждающее ощущение причастности к поворотному моменту в истории физики. Многие из нас засиживались глубоко за полночь, штудируя увесистые фолианты по теоретической физике и абстрактной математике, знание которых необходимо для понимания теории струн.

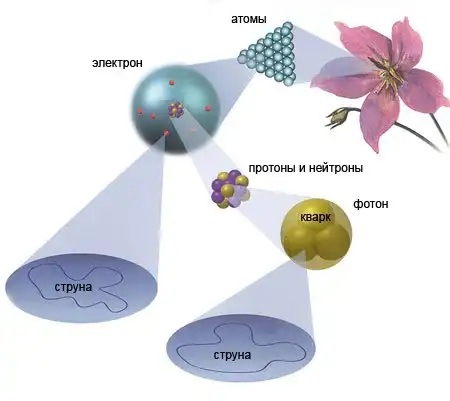
Если верить учёным, то мы сами и всё вокруг нас состоит из
бесконечного множества вот таких загадочных свернутых микрообъектов.

Период с 1984 по 1986 гг. теперь известен как «первая революция в теории суперструн». В течение этого периода физиками всего мира было написано более тысячи статей по теории струн. Эти работы окончательно продемонстрировали, что многочисленные свойства стандартной модели, открытые в течение десятилетий кропотливых исследований, естественным образом вытекают из величественной системы теории струн. Как заметил Майкл Грин, «момент, когда вы знакомитесь с теорией струн и осознаете, что почти все основные достижения физики последнего столетия следуют – и следуют с такой элегантностью – из столь простой отправной точки, ясно демонстрирует вам всю невероятную мощь этой теории»5. Более того, для многих из этих свойств, как мы увидим ниже, теория струн дает гораздо более полное и удовлетворительное описание, чем стандартная модель. Эти достижения убедили многих физиков, что теория струн способна выполнить свои обещания и стать окончательной объединяющей теорией.

Двумерная проекция трехмерного многообразия Калаби-Яу. Эта проекция дает представление о том, как сложно устроены дополнительные измерения

Однако на этом пути занимавшиеся теорией струн физики снова и снова натыкались на серьезные препятствия. В теоретической физике часто приходится иметь дело с уравнениями, которые либо слишком сложны для понимания, либо с трудом поддаются решению. Обычно в такой ситуации физики не пасуют и пытаются получить приближенное решение этих уравнений. Положение дел в теории струн намного сложнее. Даже сам вывод уравнений оказался столь сложным, что до сих пор удалось получить лишь их приближенный вид. Таким образом, физики, работающие в теории струн, оказались в ситуации, когда им приходится искать приближенные решения приближенных уравнений. После нескольких лет поражающего воображение прогресса, достигнутого в течение первой революции теории суперструн, физики столкнулись с тем, что используемые приближенные уравнения оказались неспособными дать правильный ответ на ряд важных вопросов, тормозя тем самым дальнейшее развитие исследований. Не имея конкретных идей по выходу за рамки этих приближенных методов, многие физики, работавшие в области теории струн, испытали растущее чувство разочарования и вернулись к своим прежним исследованиям. Для тех, кто остался, конец 1980-х и начало 1990-х гг. были периодом испытаний.

Красота и потенциальная мощь теории струн манили исследователей подобно золотому сокровищу, надежно запертому в сейфе, видеть которое можно лишь через крошечный глазок, но ни у кого не было ключа, который выпустил бы эти дремлющие силы на свободу. Долгий период «засухи» время от времени прерывался важными открытиями, но всем было ясно, что требуются новые методы, которые позволили бы выйти за рамки уже известных приближенных решений.

Конец застою положил захватывающий дух доклад, сделанным Эдвардом Виттеном в 1995 г. на конференции по теории струн в университете Южной Калифорнии – доклад, который ошеломил аудиторию, до отказа заполненную ведущими физиками мира. В нем он обнародовал план следующего этапа исследований, положив тем самым начало «второй революции в теории суперструн». Сейчас специалисты по теории струн энергично работают над новыми методами, которые обещают преодолеть встреченные препятствия.



За широкую популяризацию ТС человечеству стоило бы поставить памятник профессору Колумбийского университета (Columbia University) Брайану Грину (Brian Greene). Его вышедшая в 1999 году книга «Элегантная Вселенная. Суперструны, скрытые размерности и поиски окончательной теории» стала бестселлером и получила Пулитцеровскую премию. Труд учёного лёг в основу научно-популярного мини-сериала с самим автором в роли ведущего – его фрагмент можно увидеть в конце материала (фото Amy Sussman/Columbia University).

А теперь давайте хоть немного попробуем понять суть этой теории.

Начнём с начала. Нулевое измерение — это точка. У неё нет размеров. Двигаться некуда, никаких координат для обозначения местонахождения в таком измерении не нужно.
Поставим рядом с первой точкой вторую и проведём через них линию. Вот вам и первое измерение. У одномерного объекта есть размер — длина, но нет ни ширины, ни глубины. Движение в рамках одномерного пространства очень ограничено, ведь возникшее на пути препятствие не обойдёшь. Чтобы определить местонахождение на этом отрезке, понадобится всего одна координата.

Поставим рядом с отрезком точку. Чтобы уместить оба эти объекта, нам потребуется уже двумерное пространство, обладающее длиной и шириной, то есть, площадью, однако без глубины, то есть, объёма. Расположение любой точки на этом поле определяется двумя координатами.

Третье измерение возникает, когда мы добавляем к этой система третью ось координат. Нам, жителям трёхмерной вселенной, очень легко это представить.

Попробуем вообразить, как видят мир жители двухмерного пространства. Например, вот эти два человечка:















Именно смена точки обзора позволяет нашим героям судить друг о друге как о двумерных объектах, а не одномерных отрезках.

А теперь представим, что некий объёмный объект движется в третьем измерении, которое пересекает этот двумерный мир. Для стороннего наблюдателя, это движение выразится в смене двумерных проекций объекта на плоскости, как у брокколи в аппарате МРТ:



Но для обитателя нашей Флатландии такая картинка непостижима! Он не в состоянии даже представить её себе. Для него каждая из двумерных проекций будет видеться одномерным отрезком с загадочно переменчивой длиной, возникающим в непредсказуемом месте и также непредсказуемо исчезающим. Попытки просчитать длину и место возникновения таких объектов с помощью законов физики двумерного пространства, обречены на провал.

Мы, обитатели трёхмерного мира, видим всё двумерным. Только перемещение предмета в пространстве позволяет нам почувствовать его объём. Любой многомерный объект мы увидим также двумерным, но он будет удивительным образом меняться в зависимости от нашего с ним взаиморасположения или времени.

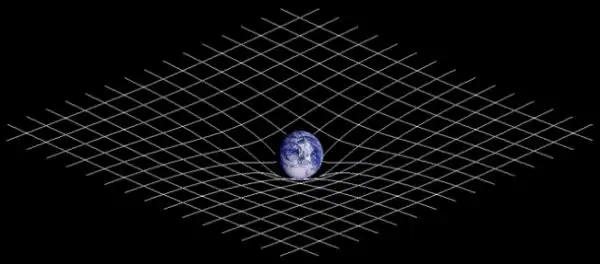
С этой точки зрения интересно думать, например, про гравитацию. Все, наверное, видели, подобные картинки:



На них принято изображать, как гравитация искривляет пространство-время. Искривляет… куда? Точно ни в одно из знакомых нам измерений. А квантовое туннелирование, то есть, способность частицы исчезать в одном месте и появляться совсем в другом, причём за препятствием, сквозь которое в наших реалиях она не смогла бы проникнуть, не проделав в нём дыру? А чёрные дыры? А что, если все эти и другие загадки современной науки объясняются тем, что геометрия пространства совсем не такая, какой мы привыкли её воспринимать?

Тикают часики

Время добавляет к нашей Вселенной ещё одну координату. Для того, чтобы вечеринка состоялась, нужно знать не только в каком баре она произойдёт, но и точное время этого события.

Исходя из нашего восприятия, время — это не столько прямая, как луч. То есть, у него есть отправная точка, а движение осуществляется только в одном направлении — из прошлого в будущее. Причём реально только настоящее. Ни прошлое, ни будущее не существуют, как не существуют завтраки и ужины с точки зрения офисного клерка в обеденный перерыв.

Но теория относительности с этим не согласна. С её точки зрения, время — это полноценное измерение. Все события, которые существовали, существуют и будут существовать, одинаково реальны, как реален морской пляж, независимо от того, где именно мечты о шуме прибоя захватили нас врасплох. Наше восприятие — это всего лишь что-то вроде прожектора, который освещает на прямой времени какой-то отрезок. Человечество в его четвёртом измерении выглядит приблизительно так:



Но мы видим только проекцию, срез этого измерения в каждый отдельный момент времени. Да-да, как брокколи в аппарате МРТ.

До сих пор все теории работали с большим количеством пространственных измерений, а временное всегда было единственным. Но почему пространство допускает появление множественных размерностей для пространства, но время только одно? Пока учёные не смогут ответить на этот вопрос, гипотеза о двух или более временных пространствах будет казаться очень привлекательной всем философам и фантастам. Да и физикам, чего уж там. Скажем, американский астрофизик Ицхак Барс корнем всех бед с Теорией Всего видит как раз упущенное из виду второе временное измерение. В качестве умственного упражнения, попробуем представить себе мир с двумя временами.

Каждое измерение существует отдельно. Это выражается в том, что если мы меняем координаты объекта в одной размерности, координаты в других могут оставаться неизменными. Так, если вы движетесь по одной временной оси, которая пересекает другую под прямым углом, то в точке пересечения время вокруг остановится. На практике это будет выглядеть приблизительно так:



Всё, что Нео нужно было сделать — это разместить свою одномерную временную ось перпендикулярно временной оси пуль. Сущий пустяк, согласитесь. На самом деле всё намного сложнее.

Точное время во вселенной с двумя временными измерениями будет определяться двумя значениями. Слабо представить себе двумерное событие? То есть, такое, которое протяжённо одновременно по двум временным осям? Вполне вероятно, что в таком мире потребуются специалисты по составлению карты времени, как картографы составляют карты двухмерной поверхности земного шара.

Что ещё отличает двумерное пространство от одномерного? Возможность обходить препятствие, например. Это уже совсем за границами нашего разума. Житель одномерного мира не может представить себе как это — завернуть за угол. Да и что это такое — угол во времени? Кроме того, в двумерном пространстве можно путешествовать вперёд, назад, да хоть по диагонали. Я без понятия как это — пройти через время по диагонали. Я уж не говорю о том, что время лежит в основе многих физических законов, и как изменится физика Вселенной с появлением ещё одного временного измерения, невозможно представить. Но размышлять об этом так увлекательно!

Очень большая энциклопедия

Другие измерения ещё не открыты, и существуют только в математических моделях. Но можно попробовать представить их так.

Как мы выяснили раньше, мы видим трёхмерную проекцию четвёртого (временного) измерения Вселенной. Другими словами, каждый момент существования нашего мира — это точка (аналогично нулевому измерению) на отрезке времени от Большого взрыва до Конца Света.

Те из вас, кто читал про перемещения во времени, знают какую важную роль в них играет искривление пространственно-временного континуума. Вот это и есть пятое измерение — именно в нём «сгибается» четырёхмерное пространство-время, чтобы сблизить две какие-то точки на этой прямой. Без этого путешествие между этими точками было бы слишком длительным, или вообще невозможным. Грубо говоря, пятое измерение аналогично второму — оно перемещает «одномерную» линию пространства-времени в «двумерную» плоскость со всеми вытекающими в виде возможности завернуть за угол.

Наши особо философско-настроенные читатели чуть ранее, наверное, задумались о возможности свободной воли в условиях, где будущее уже существует, но пока ещё не известно. Наука на этот вопрос отвечает так: вероятности. Будущее — это не палка, а целый веник из возможных вариантов развития событий. Какой из них осуществится — узнаем когда доберёмся.

Каждая из вероятностей существует в виде «одномерного» отрезка на «плоскости» пятого измерения. Как быстрее всего перескочить из одного отрезка на другой? Правильно — согнуть эту плоскость, как лист бумаги. Куда согнуть? И снова правильно — в шестом измерении, которое придаёт всей этой сложной структуре «объём». И, таким образом, делает её, подобно трёхмерному пространству, «законченной», новой точкой.

Седьмое измерение — это новая прямая, которая состоит из шестимерных «точек». Что представляет собой какая-либо другая точка на этой прямой? Весь бесконечный набор вариантов развития событий в другой вселенной, образованной не в результате Большого Взрыва, а в других условиях, и действующей по другим законам. То есть, седьмое измерение — это бусы из параллельных миров. Восьмое измерение собирает эти «прямые» в одну «плоскость». А девятое можно сравнить с книгой, которая уместила в себя все «листы» восьмого измерения. Это совокупность всех историй всех вселенных со всеми законами физики и всеми начальными условиями. Снова точка.

Тут мы упираемся в предел. Чтобы представить себе десятое измерение, нам нужна прямая. А какая может быть другая точка на этой прямой, если девятое измерение уже покрывает всё, что только можно себе представить, и даже то, что и представить невозможно? Получается, девятое измерение — это не очередная отправная точка, а финальная — для нашей фантазии, во всяком случае.

Теория струн утверждает, что именно в десятом измерении совершают свои колебания струны — базовые частицы, из которых состоит всё. Если десятое измерение содержит себе все вселенные и все возможности, то струны существуют везде и всё время. В смысле, каждая струна существует и в нашей вселенной, и любой другой. В любой момент времени. Сразу. Круто, ага?

Физик, специалист по теории струн. Известен своими работами по зеркальной симметрии, связанными с топологией соответствующих многообразий Калаби-Яу. Широкой аудитории известен как автор научно популярных книг. Его «Элегантная Вселенная» была номинирована на Пулитцеровскую премию.

В сентябре 2013 года в Москву по приглашению Политехнического музея приехал Брайан Грин. Знаменитый физик, специалист по теории струн, профессор Колумбийского университета, он известен широкой публике в первую очередь как популяризатор науки и автор книги «Элегантная Вселенная». «Лента.ру» поговорила с Брайаном Грином о теории струн и недавних трудностях, с которыми столкнулась эта теория, а также о квантовой гравитации, амплитуэдре и социальном контроле.

Литература на русском языке:

Литература на английском языке:
Тексты от профессионалов