Вселенная фракталов (+видео)
Сам я впервые столкнулся с фрактальными множествами более 15 лет назад. Фракталы поразили меня тогда не только своей завораживающей красотой, свойствами самоподобия и безконечности масштабирования, но и относительной простотой в реализации.
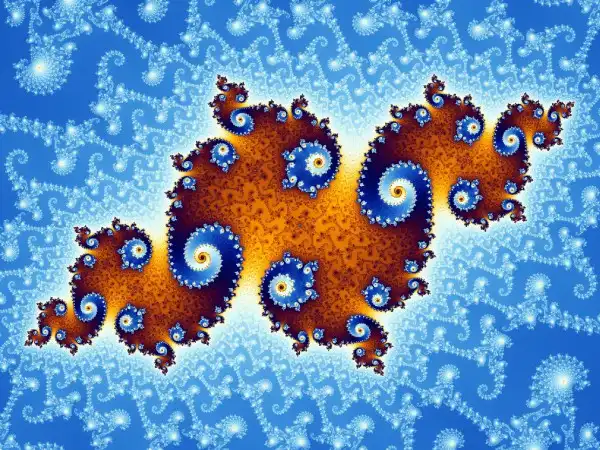
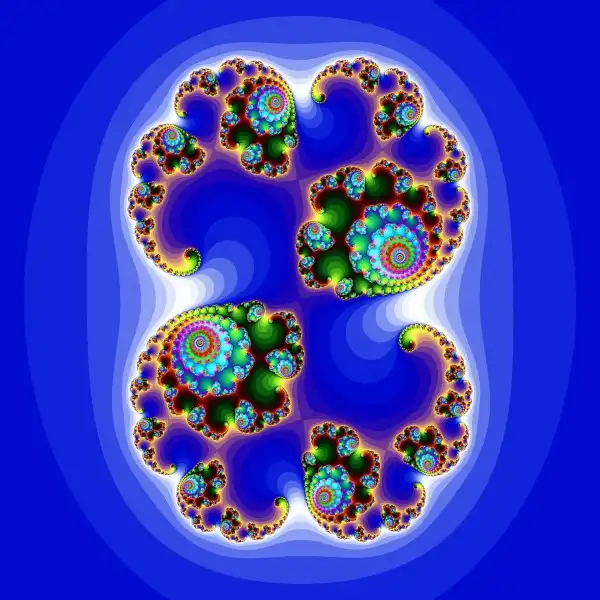
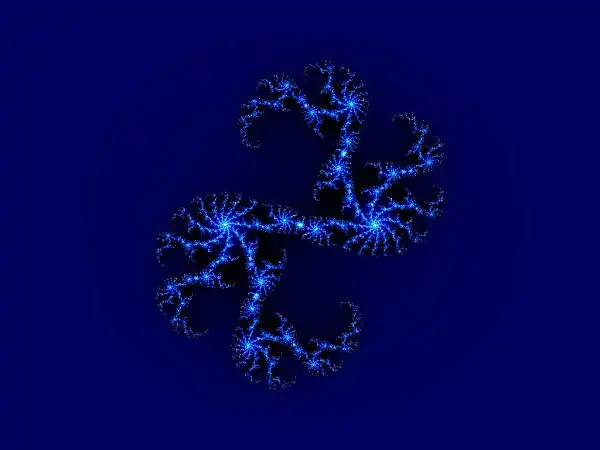
Ниже представлены изображения классических фракталов - множества Мандельброта и Жюлиа:
:: Множество Мандельброта (Mandelbrot) ::
:: Множество Жюлиа (Julia set) ::
Больше всего поражает воображение то, что весь этот безконечный мир красоты фрактальных изображений множеств Жюлиа и Мандельброта описывается на комплексной плоскости следующим весьма простым математическим выражением!!!
Z (i+1) = Z (i) ^ 2 + c
Далее предлагаю два наиболее удачных, на мой взгляд, видеоролика от Michael Hogg и SethComposerGuy, позволяющих погрузиться в мир множества Мандельброта.
(заранее прошу прощения за качество, ограничения на размер загружаемых файлов не позволяют залить видео с лучшим качеством :crybaby: , если кому будет интересно, позже могу выложить видео на hdd.tomsk.ru)
Путем нехитрых манипуляций с цветовой палитрой и величиной комплексной константы "с" можно создавать в динамике следующие формы множества Жюлиа ...
:: Геометрические фракталы полученные с использованием "методов" IFS- (IFS - Iterated Function System - система итерирующих функций) и L-систем (Lindenmayer) ::
Самыми известными фрактальными изображениями, полученными с помощью указанных систем (методов), являются квадрат и треугольник Серпинского и "лист папоротника".
Ниже короткая анимационная видеозарисовка, использующая указанные системы (методы) создания фрактальных изображений:
:: Мандельбульба (Mandelbulb) ::
Относительно недавно математиками Daniel White и Paul Nylander с использованием гиперкомплексной алгебры, основанной на сферической системе координат, был получен трехмерный аналог множества Мандельброта. Фрактал получил название Мандельбульба (Mandelbulb) или "Лампочка Мандельброта".
Ниже представлены наиболее интересные, по моему мнению, вариации на тему...