Самые крутые математические открытия - часть 2

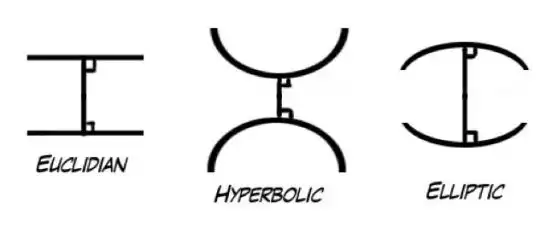
Неевклидовая геометрия

Еще один раздел математики, который вы должны помнить со школы – это геометрия, которая изучает пространственные структуры. Но большинство из нас знакомы исключительно с евклидовой геометрией, которая основывается на пяти достаточно простых аксиомах. Это самая обычная геометрия линий и точек, которые мы можем нарисовать на доске, и достаточно долго считалось, что это единственное направление, в котором может развиваться геометрия как таковая.

Проблема, однако, в том, что те очевидные аксиомы, которые изложил Евклид более двух тысяч лет назад, на самом деле на настолько всем очевидны. Одна из аксиом (постулат о параллельных прямых) никогда не устраивала математиков, и на протяжении многих веков они пытались его как-то согласовать с другими аксиомами. В начале 18 века возник принципиально новый подход: эту аксиому просто заменили на другую. Вместо пересмотра всей геометрии возникла совершенно новая гиперболическая геометрия (или геометрия Лобачевского). Это привело к полной смене парадигмы в научном сообществе и открыло ворота к возникновению разнообразных неевклидовых подходов к геометрии. Один из самых известных подходов – геометрия Римана, которая описывает ни что иное, как теорию относительности Эйнштейна (наша вселенная, что интересно, не подчиняется законам евклидовой геометрии!).




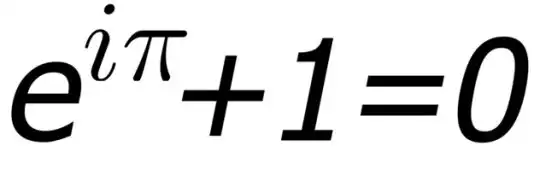
Тождество Эйлера

Тождество Эйлера – это одно из самых значительных достижений в этом списке, и принадлежит оно одному из самых продуктивных математиков в истории – Леониду Эйлеру. На протяжении своей жизни он написал более 800 работ, многие из которых – будучи уже слепым.

На первых взгляд его открытие выглядит достаточно просто: eiπ + 1 = 0. Для тех, кто не знает, e и π – это математические константы, которые где только не используются, i – это мнимое число, которое обозначает квадратный корень из -1. Самое любопытное в тождестве Эйлера то, что она объединяет все самые важные числа в математике (e, i, π, 0, 1) в одно элегантное уравнение. Физик Ричард Фейнман назвал это уравнение «самой замечательной формулой в математике». Важность этого тождества заключается в способности объединить в себе многочисленные аспекты математики.




Универсальная машина Тьюринга

Мы живем в мире, которым управляют компьютеры. Скорее всего, вы читаете эту статью именно на нем. Безусловно, компьютеры – это одно из самых важных изобретений 20-го века, но немногие знают, что компьютеры обязаны своим появлениям теоретической математике.

Математик (и криптоаналитик во время Второй мировой войны) Алан Тьюринг изобрел абстрактную вычислительную машину, которая потом получила название «машина Тьюринга». Машина Тьюринга – это примитивный компьютер, который состоит из бесконечной ленты с тремя символами (к примеру, 0, 1 и «пробел») и управляющего устройства, в которое заложен определенный набор команд. Эти команды заключаются в изменении 0 на 1, перемещении пробела влево, записи в пробеле 0 или 1, перемещении пробела вправо, и так далее. Таким образом машина Тьюринга реализует процесс пошагового вычисления, в котором каждый шаг вычисления достаточно элементарен.

Позднее Тьюринг описал Универсальную машину Тьюринга, которая может имитировать работу любой другой машины Тьюринга с заданными входными данными и программой. По сути, это прототип современных компьютерных программ. Использую только математику и логику Тьюринг создал компьютерную науку за много лет до того, как технология позволила создать настоящий компьютер.




Бесконечная бесконечность

Бесконечность сама по себе сложна для восприятия. Людям всегда достаточно сложно осмыслить это понятие, поэтому математики к бесконечности всегда относились настороженно. Так было до второй половины 19-го века, когда Георг Кантор создал теорию множеств, которая смогла помочь ему постичь истинную природу бесконечности. И то, что он открыл, поистине ошеломляет.

Как выяснилось, когда мы представляем себе бесконечность, всегда есть такая бесконечность, которая больше той, которую мы представили. Самый низкий уровень бесконечности – счетные множества, элементы которых можно пронумеровать натуральными числами. Кантор доказал, что существует более высокий порядок бесконечности – несчетные множества. Это те множества, которые не являются счетными (например, множество комплексных чисел), и если бы у вас было все время во Вселенной, вы бы не смогли их сосчитать. Но, как выяснилось, после этого уровня бесконечности существуют другие уровни. Сколько? Бесконечное количество, конечно же.




Теоремы Гёделя о неполноте

В 1931 году австрийский математик Курт Гёдель доказал две теоремы, которые просто потрясли мир математики. Вместе они доказывали достаточно печальную вещь – математика никогда не была и не будет полной.

Не вдаваясь в технические подробности, Гёдель доказал, что в любой формальной системе (например, системе натуральных чисел) существует утверждение о системе, которое средствами самой системы невозможно ни доказать, ни опровергнуть. По сути, он показал, что любая аксиоматическая система не может быть полностью автономной, что противоречило всем предыдущим математическим предположениям. Непротиворечивость достаточно богатой теории не может быть доказана средствами этой теории, но вполне может оказаться, что непротиворечивость одной конкретной теории может быть установлена средствами другой, более мощной формальной теории. Но тогда встаёт вопрос о непротиворечивости этой второй теории, и т. д. Значит, сколько бы ученые не пытались создать замкнутую на саму себя непротиворечивую систему – у них ничего не получится, система будет только увеличиваться при попытках лишить ее противоречивости.