Достижения теоретической и экспериментальной физики: искривляя пространство
То, о чем я хочу написать в этом посте, имеет отношение в основном к геометрии, нежели к физике (хотя в конечном плане тесно с ней переплетается). Но поскольку неохота разрывать отдельными рубриками прекрасную науку от еще более прекрасной (какая из этих двух более прекрасна - пусть каждый сам для себя решает), то позволю себе рассказать о великих открытиях в геометрии в рамках ранее созданной рубрики. В этом посте речь пойдет, наверно, о самом главном в мире геометрии - о том, как изменялось со временем представление человека об окружающем его пространстве, о его форме и характере.
Отмечу, что не буду здесь говорить о всяких экзотических пространствах, типа многообразий Калаби-Яу и прочих модных исследований в рамках Теории струн, просто потому, что ТС - на данный момент это что-то эфемерное, после прочтения в свое время я понял, что на данный момент это уж слишком экстравагантная теория. Да что говорить, если мы представить не можем - как изобразить трехмерную сферу...а там хотят изобразить двумерную проекцию трехмерного пространства - шестимерная фигура! В общем, мы будем проще и остановимся только на классике жанра.
Естественно, что люди поначалу все свои представления связывали лишь с одним местом - с Землей, на которой они жили. Отсюда и слово - "Геометрия" - с греческого переводится как "Измерение Земли". Конечно, люди того времени считали, что Земля плоская. Ведь они ходили по ней, они не ощущали никакой кривизны, а о размерах той плоскости, по которой они ходили, уж и подавно никто представления не имел. Но греки были умными, со временем они, по сути, добавили геометрии функциональности, сделали ее частью математики, они поняли, что мир можно постичь через математику. Грек Эратосфен одним из первых показал сферичность Земли и даже рассчитал длину ее окружности, да так рассчитал, что полученное значение практически совпадает с реальным. Кстати говоря, еще примерно лет за 100 до него, грек Аристотель подозревал, что Земля искривлена. Такие мысли ему на ум приходили, когда он наблюдал за исчезавшими за горизонтом кораблями. Он не понимал - как такое может быть, что они исчезают по частям: сначала корпус, потом мачты, потом паруса...Если Земля плоская, то они должны исчезать целиком, превращаться в точку. Но снова и снова корабли исчезали по частям...Логичным было предположить, что Земля не плоская.
Ну а что же пространство? Считается, что первым человеком, совершившим революцию в представлениях о пространстве, является Евклид. Этот человек на переделе 4 и 3 веков до н.э. написал эпический труд под названием "Начала", состоящий из кучи томов, содержащих всякие аксиомы, теоремы, постулаты, доказательства. Евклид описывал геометрию плоского пространства, и считается, что вся суть его геометрии отображается в пяти основных постулатах. Давайте кратко на них посмотрим. В современной интерпретации они звучат так:
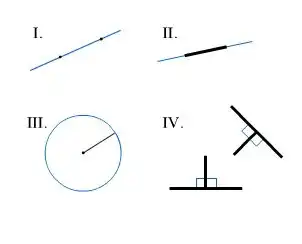
1. От всякой точки до всякой точки можно провести прямую.
Здесь все понятно и логично.
2. Ограниченную прямую можно непрерывно продолжать по прямой.
Тут вроде бы тоже никаких трудностей.
3. Из всякого центра всяким раствором может быть описан круг.
Т.е. если мы воображаемым циркулем рисуем окружность, длина радиус-вектора (в смысле отрезка между ножками циркуля) не меняется, потому что вот такое пространство само по себе.
4. Все прямые углы равны между собой.
Здесь имеется ввиду даже не то, что при пересечении двух перпендикулярных прямых все углы равны между собой, а то, что абсолютно все углы будут равны между собой при пересечении перпендикулярных прямых во всех точках пространства. Опять же, это нам говорит о том, что пространство такое, что эти линии на всем своем протяжении - именно прямые.
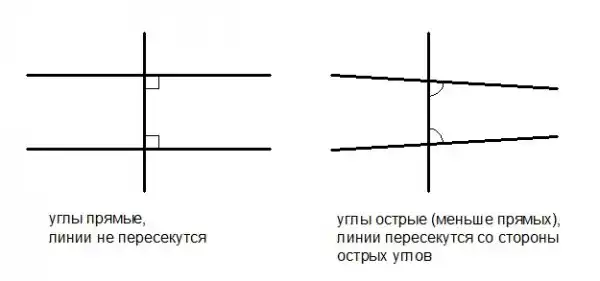
5. Если прямая, пересекающая две прямые, образует внутренние односторонние углы, меньшие двух прямых, то, продолженные неограниченно, эти две прямые встретятся с той стороны, где углы меньше двух прямых.
Сложноватая формулировка, поэтому я иллюстрировал это (рисунок ниже). Это постулат параллельности. Его не любил сам Евклид, и не любили все последующие математики. Просто он сложноват для постулата и все считали, что он требует доказательства, т.е. больше на теорему смахивает. Есть более простая формулировка постулата параллельности, которую вроде как в школе штудируют: если есть прямая и не лежащая на ней точка (но лежащая в той же плоскости), то через эту точку можно провести одну и только одну прямую, параллельную данной. Если рассматривать плоское пространство, то эта формулировка в принципе верна. Но, этот постулат может быть нарушен, если допустить, что существует не одна, а много линий, проведенных через точку, не лежащую на данной прямой. Также он может быть нарушен, если допустить, что параллельных прямых не существует вообще. Запомните последние два допущения, мы вспомним о них в дальнейшем. Жаль, что если бы школьник собрался доказать эти два допущения, у него вряд ли что-то получилось, потому что школьная геометрия ограничивается лишь плоской евклидовой доской...
И вот почти целых 2000 лет все наши представления о Вселенной и о геометрии как таковой зиждились на евклидовых постулатах, которые воспринимались по сути как факт, как просто интерпретация того, что лежит на поверхности. Правда, все эти 2000 лет единственной "занозой" сидел этот проклятый постулат параллельности, который математики пытались все время доказать, начиная с Птолемея во 2 веке н.э., который решил видоизменить формулировку постулата и в итоге вроде бы вывел исходный постулат. Сработал, так сказать, метод от противного.
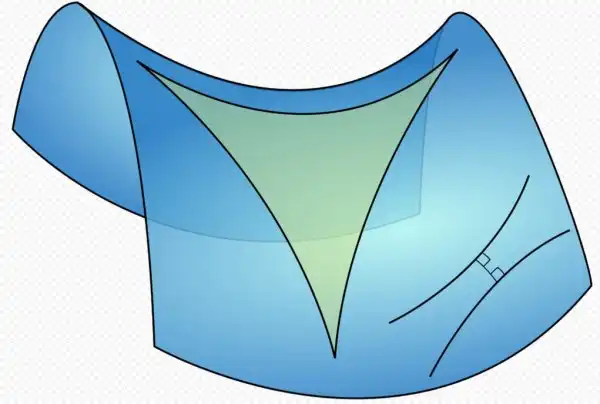
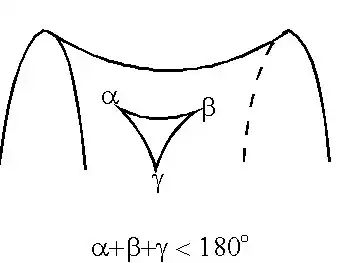
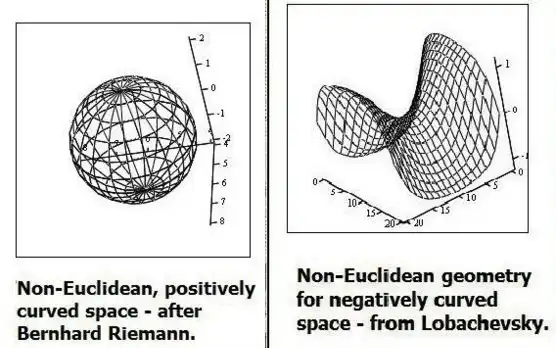
Но...в конце 18 - начале 19 века пятый постулат неожиданно рухнул, а вместе с ним рухнула вся евклидова геометрия, да и вообще вся математика, и даже физика. Удачное покушение совершил Карл Гаусс, гений, который уже в 3 года в математике разбирался лучше взрослого человека. Он составил уравнения, которые описывали части треугольника в новом пространстве, неевклидовом. Структуру этого пространства современные специалисты называют гиперболической геометрией. Многие называют это "геометрией седла", или "геометрией отрицательной кривизны", где сумма углов в треугольнике меньше 180 градусов. Кстати, спустя несколько лет, Бойяи и Лобачевский также сообщили о своих претензиях на прорывы в неевклидовой геометрии, и в отличие от Гаусса даже опубликовали свои работы, но Лобачевский сделал это в никому не известном русском журнале, а Бойяи - вообще, в какой-то из отцовых книг. Многие считают Лобачевского ключевой фигурой в создании неевклидовой геометрии, но, при всем уважении к нему, о нем бы никто не узнал, если бы не связи с Гауссом. Ведь Гаусс поступал мудро, не публикуя свои труды, тем самым избежав бесполезных прений с "натурфилософами", а эти двое, видимо, об этом не думали. К тому же, именно Гаусс выдвинул Лобачевского в член-корреспонденты Королевского научного общества Гёттингена, и того сразу же избрали.
Что же это за пространство такое - гиперболическое? Все очень просто: если мы еще раз прочитаем формулировку постулата параллельности, которую в школе штудируют, и допустим, что для любой данной прямой есть не одна, а несколько параллельных прямых, проведенных через точку, не лежащую на данной прямой, то и получится "геометрия седла". Если на гиперболическую плоскость нанести кучу треугольников разного размера (строго говоря, на такую плоскость невозможно нанести два одинаковых треугольника), то чем меньше треугольник, тем он более евклидов, т.е. угловой дефект меньше - сумма углов максимально приближается к 180 градусам. Но полной евклидости на такой поверхности никогда не достигнуть.
Но...Гауссу (и уж тем более Лобачевскому) не удалось достигнуть наглядной иллюстрации гиперболического пространства. Проще всего это получилось у всем известного физика и математика Анри Пуанкаре. Как? Да он просто заменил все эвклидовы элементы и понятия вещественными объектами. Например, то же седло. Если на такую поверхность нанести точки и линии, то линия, проведенная между двумя точками по кратчайшей траектории, так называемая геодезическая линия, будет являться аналогом обычной прямой линии, проведенной между двумя точками в евклидовом пространстве. Кроме того, если мы снова обратимся к постулату параллельности, то мы увидим, что в его гиперболической версии все меняется, и через точку, не лежащую на данной линии (уже на гиперболической поверхности) можно провести множество линий, не пересекающих данную линию. Вспомните об одном из допущений о нарушении постулата, о которых я просил запомнить! Это в корне отличается от представлений в евклидовом пространстве. Вот так все просто и наглядно представил Пуанкаре.
Спустя лет 20, один из учеников Гаусса - Георг Риман, сдал на проверку свою работу, в которой он рассматривал сферу как двухмерное эллиптическое пространство. Гаусс, изучив работу, пришел в восторг. Был открыт еще один вид неевклидовой геометрии - сферическая геометрия, "геометрия шара", "геометрия положительной кривизны". Если на такую поверхность нанести треугольники, то сумма углов будет уже больше 180 градусов, и, по аналогии с гиперболической поверхностью, чем меньше треугольник, тем меньше угловой дефект - сумма углов максимально приближается к 180 градусам. Далее, геодезической линией, т.е. кратчайшей траекторией между двумя точками на сфере, является дуга большого круга - круга, центр которого совпадает с центром сферы (это самые большие окружности сферы). Снова обращаемся к постулату параллельности. Что получается? Получается, что на сферической поверхности все большие круги пересекаются, т.е. не существует параллельных линий! Вспомните второе допущение о нарушении постулата, о котором вначале говорилось. Причем большие круги пересекаются в двух точках, расположенных на противоположных сторонах сферы. Кстати, вы все в курсе, что самолеты летают именно по дуге большого круга - это кратчайшее расстояние между двумя городами. Если поверхность Земли, представляя его эллиптическим пространством, как бы "развернуть", соединить два города прямой линией, основываясь на евклидовой геометрии, а потом свернуть поверхность обратно и полететь по проведенной траектории, то эта траектория получится намного длиннее, чем полет по дуге большого круга.
Но это еще не все. Теперь нужно сказать еще о некоторых важных моментах. Если мы вспомним другие постулаты Евклида, то их интерпретация не противоречит геометрии Гаусса. Тут мы единственным способом можем провести линию между двумя точками, мы можем неограниченно продолжить эту линию. А что же с геометрией Римана? А вот здесь появляются противоречия. Можем ли мы на сфере неограниченно продолжать линию? Нет. Длина этой линии ограничена длиной окружности большого круга. Но Риман здесь попытался исхитриться - он заявил, что этот постулат (второй) описывает не существование неограниченно длинных отрезков, а лишь показывает, что у прямых нет конца - это уже выполняется для больших кругов. В ответ математики засомневались, что это не будет противоречить другим законам. Далее, берем первый постулат. Евклид и Гаусс единственным способом рисовали линию между двумя точками, кратчайшую траекторию - у Евклида это прямая, у Гаусса - геодезическая линия. А Риман? А у него заковырка в том, что между двумя точками он может нарисовать линию двумя способами! Либо с одной стороны сферы, либо с другой. Был ряд и других противоречий, но итог один - на данный момент доказана невозможность существования эллиптического (сферического) пространства. Именно пространства, не путать с эллиптическими поверхностями! Впоследствии ряд ученых, таких как Клейн, Пуанкаре, Гильберт, пытались избавиться от этих противоречий, принимались видоизменять постулаты Евклида, подгонять их под искривленные пространства, но от всех противоречий избавиться, тем не менее, не удалось.
Несмотря на то, что некоторые моменты евклидовой геометрии были противоречивы с самого начала, Евклид начал то, что длится уже больше 2000 лет - построение логически непротиворечивой математики и осознание структуры пространства, в котором мы живем. Он заложил фундамент для этого. Геометрия Евклида основывалась на базе физически видимого пространства, она строилась на аксиомах и постулатах, которые вроде бы как не требовали доказательства, потому что были явными. Но со временем математики поняли, что для построения логически непротиворечивой структуры этот подход неверен, аксиомы требуют проверки, доказательств. В результате были открыты искривленные пространства, имеющие более строгую базу - они были облечены в математические формулы и доказательства - то, что не требовалось ученым времен Евклида. Каковы последствия этого? Например, модели искривленных пространств послужили базой для Теории относительности Эйнштейна. В его теории геометрия стала определяющей в видении нашей Вселенной. Оказалось, что траектория каждого тела во Вселенной - это следствие искривления пространства вблизи более массивных тел, таких как звезды, черные дыры, массивные планеты. Каждое тело во Вселенной думает, что оно движется по прямой, но искривленное пространство заставляет его двигаться по своей кривизне. И это не умозрительные догадки, это показано строгой и изящной математикой.