Почему в Красной армии число «пи» равно трём?
Возможно, вы слышали старую шутку о том, что «в красной армии число «π» равняется трём». Так вот, это не шутка.
Для упрощения вычислений по армейскому стрелковому уставу полагается, что «по длине окружности укладывается шесть её радиусов, или, что то же самое, три диаметра». То есть число «пи» действительно оказывается равно 3 (а не 3.14159265358... – как в учебнике математики).
Если у вас есть армейский или морской бинокль, обратите внимание на «сетку» из коротких и длинных штрихов, которую видно в окуляр – эта сетка называется «дальномерной» и служит для быстрого и довольно точного измерения расстояний, что в военном деле (например, при артиллерийской стрельбе) очень важно. Дальномерная шкала бинокля (как, впрочем, и артиллерийского или стрелкового оптического прицела) градуируется в особых единицах, которые называются «тысячными».
При измерении в тысячных каждый радиус окружности делится на 1000, таким образом одна тысячная составляет 1/6000 полной окружности, или 3' 36" (~ 3.5 угловой минуты или ~ 1/17 градуса). Дальномерная шкала бинокля обычно градуируется с шагами в 5 тысячных (0.3º) и 10 тысячных (0.6º).
Почему для дальномерной шкалы армейского бинокля была выбрана такая необычная единица измерения? Математика учит нас, что для очень малых углов тангенс с хорошей степенью приближения равен своему аргументу:
Если α<<1º, то tg α =α
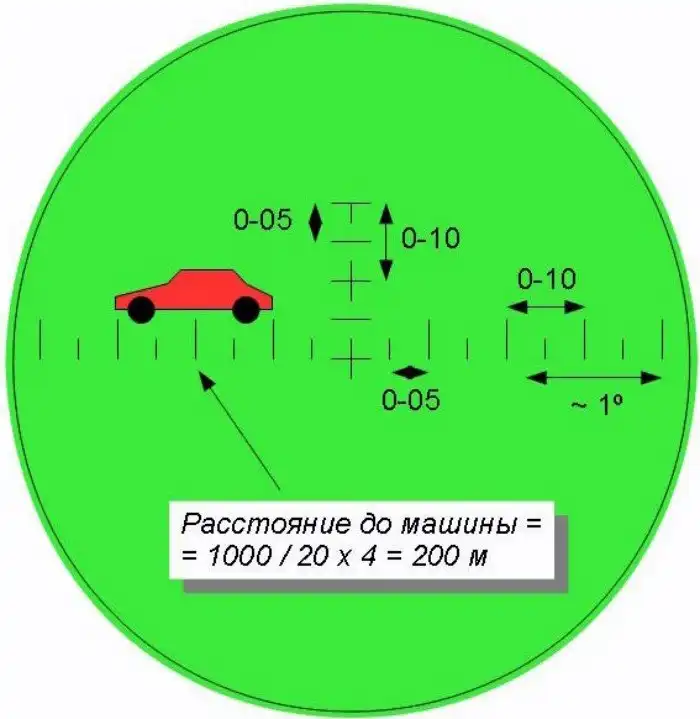
Тогда для угла в одну тысячную соблюдается соотношение в 1000:1 между расстоянием до предмета и его линейными (а не угловыми) размерами — именно поэтому шкала в тысячных и называется дальномерной. Если, скажем, мы наблюдаем в бинокль «сбоку» легковой автомобиль, длина корпуса у которого равняется 4 метрам, и он в поле зрения бинокля умещается точно в два больших деления дальномерной шкалы (то есть виден под углом 20 тысячных) тогда расстояние до него равняется
1000 : 20 х 4 = 200 метрам
(тысяча делится на количество тысячных и умножается на реальный размер объекта). В армии это правило заучивается наизусть в следующем виде: «Предмет высотой в 1 метр виден на расстоянии в 1 километр под углом в 1 тысячную».
Измерение расстояний полевым биноклем
Само собой разумеется, что для измерений с помощью дальномерной шкалы боец должен знать наизусть приблизительные размеры различных объектов. Например, высота стандартного телеграфного столба – 6 метров, 9-этажного дома – 25 метров, железнодорожного вагона – 3 с половиной метра, и так далее.
Линейные размеры людей и предметов
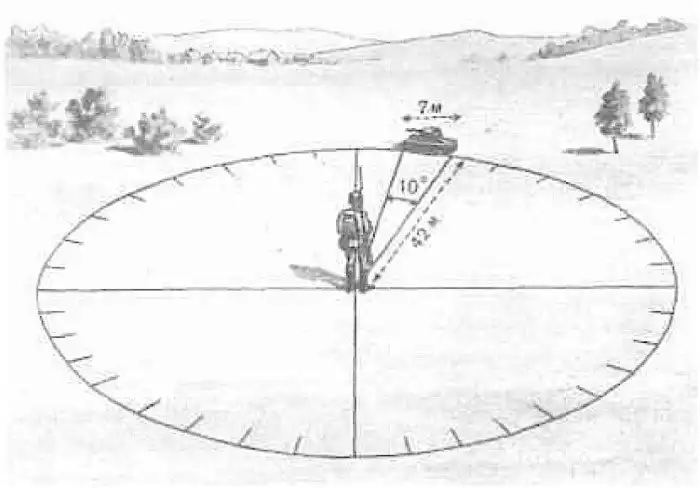
Ну и, само собой, солдату нужно уметь уверенно и быстро считать такие вот арифметические примеры в уме: если стандартный 5-этажный дом (высота 15 метров) виден в прицел/визир под углом в одно малое деление (5 тысячных), то расстояние равно 1000 : 5 x 15 = 200 x 15 = 3000 метров.
Принцип определения расстояния через видимый угол
Безусловно, для измерения расстояний используются и более точные современные приборы – скажем, лазерные или оптические дальномеры или даже GPS/ГЛОНАСС-навигаторы. Однако умение работать со старой доброй дальномерной шкалой не только может пригодиться на практике – например, при ориентировании на незнакомой местности по карте – но ещё и отлично тренирует память и математические навыки.