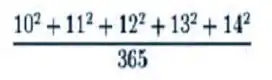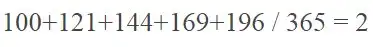Устный счет в «безграмотной России»
Знаменитый русский художник Николай Петрович Богданов-Бельский написал уникальную и невероятно жизненную историю в 1895 году. Произведение называется «Устный счёт», а в полной версии «Устный счёт. В народной школе С.А.Рачинского».
Картина написана маслом по холсту, на ней изображена сельская школа 19 века во время урока арифметики. Школьники решают интересный и сложный пример. Они находятся в глубокой задумчивости и поиске верного решения. Кто-то думает у доски, кто-то стоит в сторонке и пытается сопоставить знания, которые помогут при решении задачи. Дети полностью поглощены поиском ответа на поставленный вопрос, они хотят доказать себе и миру, что могут это сделать.
Рядом стоит учитель, прототипом которого является сам Рачинский – знаменитый ботаник и математик. Не зря картине присвоено такое название, оно в честь профессора Московского университета. На полотне изображено 11 человек детей и только один мальчик тихо шепчет учителю на ухо, возможно правильный ответ.
На картине изображён простой русский класс, дети одеты в крестьянскую одежду: лапти, штаны и рубахи. Всё это очень гармонично и лаконично вписывается в сюжет, ненавязчиво неся миру тягу к знаниям со стороны простого русского народа.
Тёплая цветовая гамма несёт доброту и простоту русского народа, здесь нет зависти и фальши, нет зла и ненависти, дети из разных семей с разным достатком собрались воедино для принятия единственно верного решения. Этого очень не хватает в нашей современной жизни, где люди привыкли жить совсем по – другому, не считаясь, с мнением окружающих.
Николай Петрович посвятил картину своему учителю, великому гению математики, которого хорошо знал и уважал. Сейчас картина находится в Москве в Третьяковской галерее, будете там, обязательно взгляните на перо великого мастера.
На картине изображён простой русский класс, дети одеты в крестьянскую одежду: лапти, штаны и рубахи. Всё это очень гармонично и лаконично вписывается в сюжет, ненавязчиво неся миру тягу к знаниям со стороны простого русского народа.
Тёплая цветовая гамма несёт доброту и простоту русского народа, здесь нет зависти и фальши, нет зла и ненависти, дети из разных семей с разным достатком собрались воедино для принятия единственно верного решения. Этого очень не хватает в нашей современной жизни, где люди привыкли жить совсем по – другому, не считаясь, с мнением окружающих.
Николай Петрович посвятил картину своему учителю, великому гению математики, которого хорошо знал и уважал. Сейчас картина находится в Москве в Третьяковской галерее, будете там, обязательно взгляните на перо великого мастера.
А теперь самое главное, вы сможете в уме решить задачку, которая написана на доске?
Вот вам поближе это математическое выражение:
Так, в уме я конечно считать не буду, потому что не смогу, а вот что получается на калькуляторе:
Так есть ли тут какая то хитрость, чтобы это посчитать в уме?
Пожалуйста оцените статью и поделитесь своим мнением в комментариях — это очень важно для нас!
Комментарии7
