Самые трудные в мире задачки

Вот некоторые из тех, что называются самыми интересными и трудными.

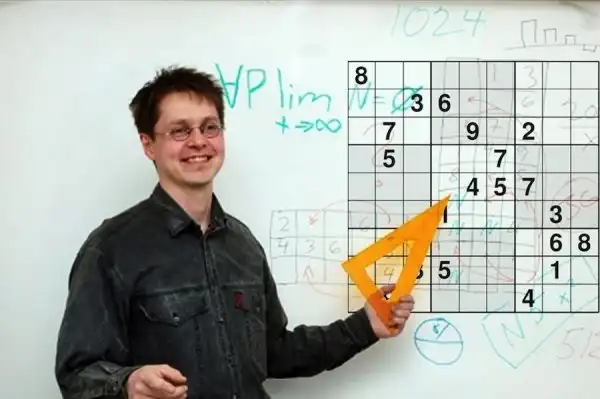
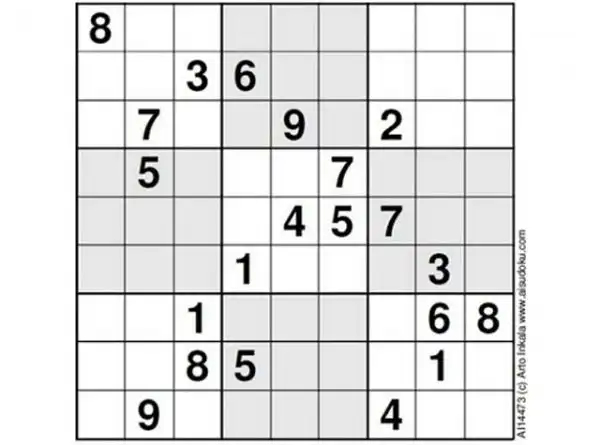
Посмотрите например на Самую трудную в мире судоку

Одной из самых популярных в мире разновидностей кроссворда является судоку — японская головоломка с числами. Её принцип несложен, поэтому многие любители стараются создать свои варианты. В 2012-м году финский математик Арто Инкала заявил, что разработал «самую трудную в мире судоку».



Как сообщает британская газета «The Telegraph», если самые простые из распространённых вариантов судоку по шкале сложности обозначить, как «1», а наиболее сложные из популярных оценить на «5», то предложенный математиком вариант тянет на «11».

Самая сложная логическая головоломка

Есть три бога, A, B, и C, один из которых бог истины, другой бог лжи и третий бог случая, причём неясно, кто из них кто. Бог истины всегда говорит правду, бог лжи обманывает, а бог случая может сказать и то, и другое в произвольном порядке. Необходимо определить, кем является каждый из богов, задав три вопроса, на которые можно ответить «да» или «нет», при этом каждый вопрос задаётся только одному богу. Боги понимают вопросы, но отвечают на своём языке, в котором есть слова «da» и «ja», но неизвестно, какое слово обозначает «да», а какое «нет».

Эта логическая задача за авторством американского философа и логика Джорджа Булоса была впервые опубликована в итальянской газете «la Repubblica» в 1992-м году. В комментариях к загадке Булос делает важное замечание: каждому богу можно задать более одного вопроса, но больше трёх задавать нельзя.



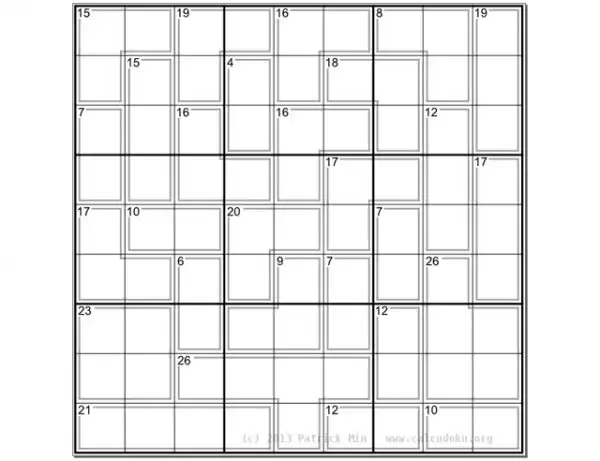
Одной из популярных разновидностей судоку является сум-до-ку, её ещё называют «убийца судоку». Вся разница в том, что в сум-до-ку заданы дополнительные числа — суммы значений в группах клеток, при этом числа, содержащиеся в группе, не должны повторяться. В популярном сервисе головоломок Calcudoku.org можно отследить рейтинг сложности опубликованных задач, одной из них стала сум-до-ку, которая изображена здесь.

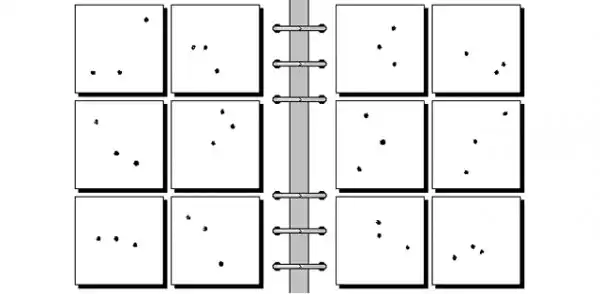
Самая сложная «Проблема узнавания» Бонгарда

Этот тип головоломки изобрёл выдающийся русский кибернетик, основоположник теории распознавания образов Михаил Моисеевич Бонгард: в 1967-м году он впервые опубликовал одну из них в своей книге «Проблема узнавания». Широкую популярность «проблемы Бонгарда» обрели, когда знаменитый американский физик и информатик Дуглас Хофштадтер упомянул о них в своём труде «Гёдель, Эшер, Бах: эта бесконечная гирлянда».

Одна из задач Мартина Гарднера

Американский математик Мартин Гарднер — автор множества самых разнообразных задач и головоломок. Одна из самых интересных его работ — вычисление числа, для которого понадобится наименьшее количество шагов, чтобы свести его к одной цифре посредством перемножения цифр этого числа. Например, для числа 77 потребуется четыре таких шага: 77 — 49 — 36 — 18 — 8. Количество шагов Гарднер называет «числом стойкости».

Наименьшее из чисел с числом стойкости, равным одному, — 10, для числа стойкости 2 это будет 25, самое маленькое число со стойкостью 3 — 39, если число стойкости равно 4, наименьшим числом для него будет 77. Каково наименьшее число с числом стойкости 5?

Самая интересная проблема из игры го

Го была придумана в Китае более 2,5 тыс лет назад, так что это одна из самых древних игр на Земле. Несмотря на достаточно простые правила, она по-прежнему привлекает тысячи людей возможностью решения интересных стратегических задач. Цель игры — огородить камнями своего цвета большую территорию, чем противник. Изображённая выше ситуация — одна из самых сложных в истории го: на её решение опытнейшие игроки потратили более 1 тыс часов игрового времени. Каким образом в этой партии могут победить чёрные?