Интересные факты: Теорема о бесконечных обезьянах

Если перенести данные рассуждения в обозримый масштаб, то теорема будет гласить — если в течение продолжительного времени случайным образом стучать по клавиатуре, то среди набираемого текста будут возникать осмысленные слова, словосочетания и даже предложения.

Эта теорема не объясняет ничего относительно интеллекта конкретной случайной обезьяны, которой посчастливится набить правильный текст. Нет никакой необходимости в обезьянах и пишущих машинках, эксперимент может быть реализован, например, подключением генератора случайных чисел к принтеру. Один из вариантов использования данной теоремы — демонстрация бытовой нелепости случайного возникновения жизни.

Теорема в полушутливой форме может быть перенесена на выбор метода грубой силы в производстве; тогда она будет звучать так: при достаточном количестве ресурсов любая техническая задача решаема. В данном случае игнорируется ограниченность ресурсов.

Логическая часть теоремы может быть перенесена на всю вселенную, тогда она будет звучать так: «В случае, если вселенная бесконечна в пространстве и/или во времени, то всё, что бы вы ни вообразили, обязательно реализуется где-то во вселенной». Доказывается она исходя из того, что вероятность возникновения любой вообразимой структуры крайне мала, но все же больше нуля, и при бесконечном количестве попыток после крайне большого, но ограниченного их числа окажется равной единице.

Теорема впервые была популяризована астрономом сэром Артуром Эддингтоном. Она стала частью идиоматических выражений благодаря научно-фантастическому рассказу «Несгибаемая логика» (Inflexible Logic) Рассела Малони (Russell Maloney), а также упоминалась в «Автостопом по галактике» Дугласа Адамса:

— Форд! — выговорил он, — там, снаружи, бесконечно много обезьян.
И они хотят обсудить с нами «Гамлета», который у них получился.

Теорема эта, строго говоря, тривиальна и не имеет особого научного значения, её популярность в массах объясняется видимой парадоксальностью.

Доказательство
По лемме Бореля — Кантелли, если два события статистически независимы, а результат одного события не влияет на результат другого, то вероятность обоих событий равняется произведению вероятностей всех участвующих событий. Например, если вероятность выпадения определённого числа в кости равняется 1/6, а шанс выигрыша в рулетке 1/38, то вероятность выигрыша в двух играх одновременно равна 1/6 × 1/38 = 1/228.

Теперь, предположите, что пишущая машинка имеет 50 клавиш, а слово, которое должно быть напечатано — «банан». При печатании наугад вероятность того, что первым напечатанным символом является «б», равна 1/50; такова же вероятность того, что вторым напечатанным символом будет «а», и так далее. Эти события независимы; таким образом, вероятность того, что первые пять букв составят слово «банан», равна (1/50)5.

По той же самой причине вероятность того, что следующие 5 букв будут словом «банан», также (1/50)5, и так далее.

Далее, вероятность того, что блок из 5 букв не является словом «банан», равен 1 − (1/50)5. Поскольку каждый блок напечатан независимо, вероятность того, что ни один из первых n блоков по 5 букв не совпадает со словом «банан», равна
P = (1 − (1/50)5)n.

Если n растет, то P становится меньше.



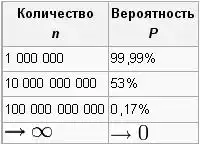
Та же самая формула применяется для любой другой строки символов конечной длины.

Это показывает, почему среди очень большого количества обезьян найдётся такая, которая будет точно воспроизводить данный текст (например, «Гамлета»). В этом случае P = (1 − (1/50)5)n, где P представляет вероятность, что ни одна из n обезьян не напечатала «банан» правильно с первой попытки. Если в эксперименте участвует сто миллиардов обезьян, вероятность падает до 0,17 %, и когда количество обезьян n стремится к бесконечности, значение P (вероятность того, что ни одна из n обезьян не смогла воспроизвести данный текст) стремится к нулю. Если заменить слово «банан» на текст «Гамлета», показатель степени увеличится с 5 до числа символов в этом тексте, но принципиально ничего не изменится, лишь понадобится большее n для сохранения того же P.

Это эквивалентно утверждению, что вероятность того, что бесконечное количество обезьян напечатают любой данный текст с первой попытки, равна 1. Другое эквивалентное утверждение: работающая бесконечно долго обезьяна-машинистка рано или поздно напечатает любой наперёд заданный текст конечной длины (например, текст этой статьи).