Основы логарифмов: понимание функции
Представьте, что вам понравилась компьютерная игра. И вы играли в неё несколько дней без перерыва. А потом пригласил в игру двоих друзей. Им игра тоже понравилась, но... возникла проблема!

Нет-нет, не такая. Мирная проблема. Вы-то уже достигли пятого уровня, а у друзей персонажи только первого уровня, слабенькие! Как им вас догнать, чтобы играть втроём?
Вы, конечно, можете удалить своего старого игрового персонажа, и начать игру заново. Или можете перестать играть и подождать, пока друзья доберутся до вашего уровня. Всё верно. Но... ску-у-учно! Однако есть и третий вариант – математический.
(В конце концов, любая компьютерная игра – это чистая математика. И если хотите научиться создавать видеоигры сами, то советуем с математикой подружиться заранее.)
Итак, чтобы перейти на следующий уровень, игроку в игре нужно набирать очки, то есть опыт, на тайном (непонятном родителям) игровом языке – «экспу». Скажем, за выполнение задания игрок получает сто очков опыта. А для прохода на второй уровень нужно набрать тысячу очков. На третий уровень – ещё тысячу, и так далее.
Такой рост уровня игрока в математике называется «линейным». Простая система, удобная и понятная – но! С ней товарища не догонишь, хоть ты тресни!
А теперь представим себе такой режим прохождения игры: для получения второго уровня игроку нужно набрать тысячу очков. А вот для получения второго – уже две тысячи! Для третьего – четыре тысячи. Для четвёртого – восемь и так далее.
Значит, чтобы перейти с пятого уровня на шестой, вам нужно набрать тридцать две тысячи очков. А друзьям, чтобы «докачаться» с первого уровня до пятого, понадобится 1+2+4+8+16 = тридцать одна тысяча очков! И они очень даже быстро (буквально за день) вас догонят, и дальше вы будете играть вместе на одном уровне!
Такой рост уровня игрока в математике называется (нетрудно догадаться) «нелинейным». Или – «логарифмическим».
Школьная линейка с её сантиметрами и миллиметрами – это линейная шкала:

1 сантиметр – 10 миллиметров. 2 сантиметра – 20 миллиметров. 3 сантиметра – 30 миллиметров. И так далее. А теперь представьте себе, что у нас вот какая причудливая шкала:
1 сантиметр – 20 миллиметров, 2 сантиметра – 40 миллиметров, 3 сантиметра – 80!.. Вот это и будет шкала «нелинейная», «логарифмическая».
Вы не представляете, насколько в науке и технике распространены такие вот «нелинейные линейки».
- Скажем, «шкала Рихтера», по которой измеряют силу землетрясений – логарифмическая.
- Шкала громкости звука в децибелах – логарифмическая.
- Яркость звёзд в астрономии – тоже.
- Время выдержки в фотоаппарате – тоже! И так далее, и так далее!
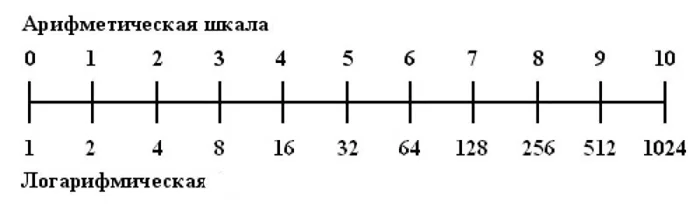
Составим таблицу с двумя рядами чисел. В верхней строчке – просто числа от нуля до девяти. А вот во второй – числа «хитрые».

Что же в них хитрого? А то, что мы можем умножать их, не умножая !
Скажем, сколько будет восемь умножить на тридцать два, сможете быстро посчитать в уме? А теперь смотрите: в нашей таблице число 8 во второй строке стоит под цифрой 3 в первой строке, а число 32 во второй строке – под цифрой 5 в первой строке, так? Сложим 3 и 5 – сколько получается? Восемь! А теперь – какое число в нашей таблице во второй строке стоит под цифрой 8 в первой строке? Число 256! Всё, вот вам и ответ!
Может, это случайное совпадение? Нет, не совпадение. Повторим опыт – умножим по нашей таблице 16 на 64.

Число 16 – под цифрой 4, число 64 – под цифрой 6. Складываем 4+6, получаем 10. А какое число у нас во второй строке под цифрой 10? Число 1024. Проверяем на калькуляторе – и правда 1024!
Так что это совсем не совпадение, а наоборот – самый настоящий математический закон. Открыли его, кстати, давным давно. И догадались, что с помощью такой вот таблицы (только более подробной, конечно) можно вместо умножения чисел использовать сложение.
«А можно вместо деления по такой волшебной таблице использовать вычитание?» – спросят самые догадливые.
А вы попробуйте. Скажем, разделить 2048 на 128 – сколько будет? 2048 стоит под цифрой 11, а 128 – под цифрой 7.

Сколько будет из одиннадцати вычесть семь? Четыре. Находим число 4 в первой строке, а под ним видим число 16. И это на самом деле правильный ответ!
Понятно, что складывать и вычитать намного проще, чем умножать и делить. Особенно если числа большие и длинные! Причём не только людям – но и компьютерам! (Да-да, бывают такие задачи в математике, физике, технике и вообще в науке, которые даже для решения на самом супербыстром компьютере желательно «упрощать».) А уж как страдали учёные в те времена, когда вообще никаких компьютеров не было! Некоторые вычисления приходилось делать недели и месяцы! Горы исписанной бумаги, вёдра чернил!
Так что же такое «логарифм»? А это как раз число из первой строчки нашей чудо-таблицы!
Мы с вами как говорили? «Число 128 в таблице стоит под номером 7». А математик скажет так: «Число 7 – это логарифм числа 128 по основанию 2».
Английский математик Джон Непер первым в мире составил такие «волшебные таблицы» в 1614 году, в книге, которая так и называлась: «Описание удивительной таблицы логарифмов», по-латыни «Мирифици логаритморум канонис дескрипцио».

В тогдашнем научном мире эта книга произвела настоящий фурор, стала бестселлером! С её помощью считали мореплаватели и строители, военные и купцы, финансисты и инженеры. Вот как об изобретении логарифмов писал знаменитый французский астроном Пьер-Симон Лаплас:
«...это удивительное искусство, которое, позволяя за несколько дней сделать работу нескольких месяцев, вдвое продлевает жизнь астроному, избавляя его от ошибок, неизбежных при долгих вычислениях...»
Само название «логарифм» происходит от греческих слов «λόγος» (логос, «разум») и «ἀριθμός» (арифмос, «число») – то есть, в переводе с греческого, «логарифмы» – это «умные числа». А ведь и правда неглупые, а?
Кстати, именно на логарифмах основана работа «деревянного калькулятора», дедушкиной (и прадедушкиной) логарифмической линейки.
